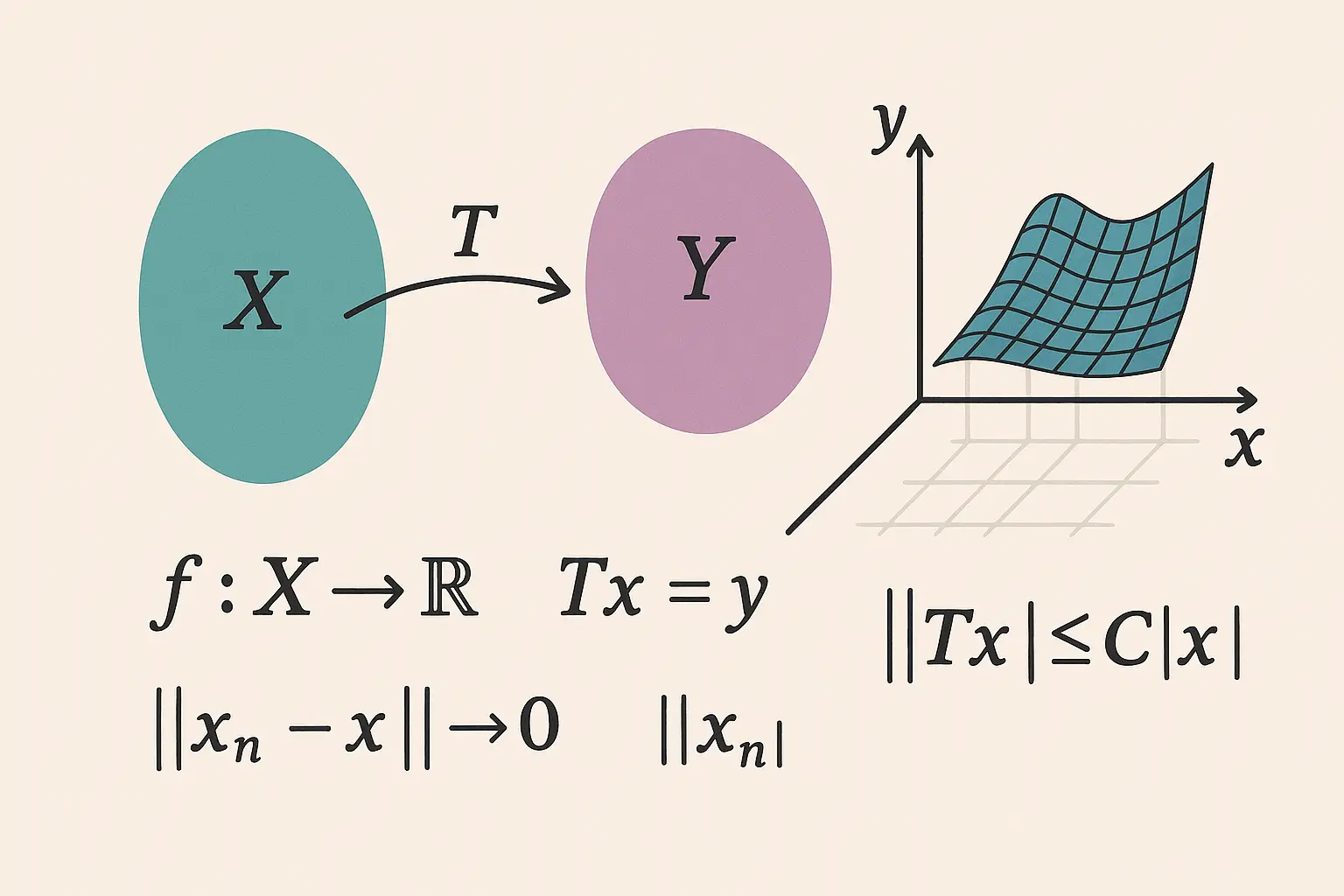Functional Analysis Basics: Infinite-Dimensional Vector Spaces and Operators

Table of Contents

1. Introduction
2. What Is Functional Analysis?
3. Normed and Banach Spaces
4. Inner Product and Hilbert Spaces
5. Linear Operators and Functionals
6. Bounded and Unbounded Operators
7. Dual Spaces and the Hahn–Banach Theorem
8. The Riesz Representation Theorem
9. Compact Operators and Spectral Theory
10. Self-Adjoint, Unitary, and Normal Operators
11. Hilbert–Schmidt and Trace Class Operators
12. Fourier Analysis in Hilbert Spaces
13. Applications to PDEs and Quantum Mechanics
14. Weak and Strong Convergence
15. Conclusion

1. Introduction

Functional analysis generalizes linear algebra and calculus to infinite-dimensional vector spaces. It is the mathematical foundation of quantum mechanics, partial differential equations (PDEs), and signal processing. It brings together vector spaces, topology, and linear operators in a unified framework.

2. What Is Functional Analysis?

Functional analysis studies vector spaces of functions and linear operators acting on them. Central themes include:

• Infinite-dimensional spaces
• Continuity and boundedness
• Spectral theory of operators
• Duality and convergence

3. Normed and Banach Spaces

A normed vector space \( (X, |\cdot|) \) is a vector space with a norm satisfying:

1. \( |x| \ge 0 \), and \( |x| = 0 \iff x = 0 \)
2. \( |\alpha x| = |\alpha||x| \)
3. \( |x + y| \le |x| + |y| \) (triangle inequality)

A Banach space is a complete normed space — all Cauchy sequences converge.

4. Inner Product and Hilbert Spaces

An inner product \( \langle x, y \rangle \) satisfies:

1. \( \langle x, x \rangle \ge 0 \)
2. \( \langle x, x \rangle = 0 \iff x = 0 \)
3. \( \langle x, y \rangle = \overline{\langle y, x \rangle} \)
4. Linearity in the first argument

The induced norm is \( |x| = \sqrt{\langle x, x \rangle} \)

A Hilbert space is a complete inner product space.

5. Linear Operators and Functionals

A linear operator \( T: X \to Y \) satisfies:

\[
T(\alpha x + \beta y) = \alpha T(x) + \beta T(y)
\]

A functional is a map \( f: X \to \mathbb{F} \) (usually \( \mathbb{R} \) or \( \mathbb{C} \)).

6. Bounded and Unbounded Operators

• Bounded: there exists \( C > 0 \) such that \( |Tx| \le C|x| \)
• Unbounded: no such constant exists; common in differential operators

Bounded operators are continuous; unbounded ones must be treated carefully.

7. Dual Spaces and the Hahn–Banach Theorem

The dual space \( X^* \) consists of all bounded linear functionals on \( X \).

Hahn–Banach Theorem: extends a bounded functional from a subspace to the whole space without increasing the norm.

8. The Riesz Representation Theorem

For a Hilbert space \( H \), every bounded linear functional \( f \in H^* \) is uniquely represented as:

\[
f(x) = \langle x, y \rangle \quad \text{for some } y \in H
\]

This establishes an isomorphism between \( H \) and \( H^* \).

9. Compact Operators and Spectral Theory

A compact operator maps bounded sets to relatively compact sets. In Hilbert spaces, these operators resemble matrices with countable spectra.

Spectral theory studies eigenvalues and eigenvectors of operators:

• Spectrum \( \sigma(T) \): generalization of eigenvalues
• Resolvent set: \( \lambda \in \mathbb{C} \) where \( (T – \lambda I)^{-1} \) exists

10. Self-Adjoint, Unitary, and Normal Operators

• Self-adjoint: \( T = T^* \)
• Unitary: \( T^T = TT^ = I \)
• Normal: \( TT^* = T^*T \)

Self-adjoint operators correspond to observables in quantum mechanics.

11. Hilbert–Schmidt and Trace Class Operators

• Hilbert–Schmidt: \( \sum |Te_n|^2 < \infty \)
• Trace class: \( \sum \langle Te_n, e_n \rangle < \infty \)

These operators are compact and play a role in quantum statistical mechanics.

12. Fourier Analysis in Hilbert Spaces

In \( L^2(\mathbb{R}) \), functions can be expanded as orthonormal sums:

\[
f(x) = \sum_{n} \langle f, e_n \rangle e_n(x)
\]

Fourier basis provides a canonical orthonormal set in function spaces.

13. Applications to PDEs and Quantum Mechanics

• Weak solutions to PDEs
• Variational methods and Sobolev spaces
• Quantum observables as self-adjoint operators
• Schrödinger equation in Hilbert space form
• Spectral decomposition and time evolution

14. Weak and Strong Convergence

• Strong convergence: \( |x_n – x| \to 0 \)
• Weak convergence: \( f(x_n) \to f(x) \) for all \( f \in X^* \)

Weak convergence is weaker but still useful in compactness and variational problems.

15. Conclusion

Functional analysis provides a rigorous mathematical framework for studying infinite-dimensional systems and operators. It is indispensable in quantum mechanics, PDE theory, and modern applied mathematics. Mastery of its basic concepts is a gateway to understanding advanced theoretical frameworks in both physics and analysis.