Postulates of Quantum Mechanics: Foundations of the Quantum World

Table of Contents

1. Introduction
2. Why Postulates?
3. Postulate 1: State Vector and Hilbert Space
4. Postulate 2: Observables and Operators
5. Postulate 3: Measurement and Expectation Values
6. Postulate 4: Time Evolution and Schrödinger Equation
7. Postulate 5: Collapse of the Wavefunction
8. Postulate 6: Identical Particles and Symmetrization
9. Mathematical Framework and Examples
10. Compatibility and Commutation Relations
11. Uncertainty Principle from Postulates
12. Relation to Classical Mechanics
13. Role in Quantum Computing and Information
14. Interpretational Challenges
15. Conclusion

1. Introduction

Quantum mechanics is based on a set of fundamental postulates. These postulates form the axiomatic foundation from which all quantum phenomena emerge. Understanding these is essential for mastering both basic and advanced quantum theory.

2. Why Postulates?

• They define the rules of the quantum game
• Not derived — instead, they’re principles inferred from experiment
• Allow for a consistent mathematical structure and predictive power
• Serve as the basis for further developments in quantum field theory, quantum computation, and condensed matter physics

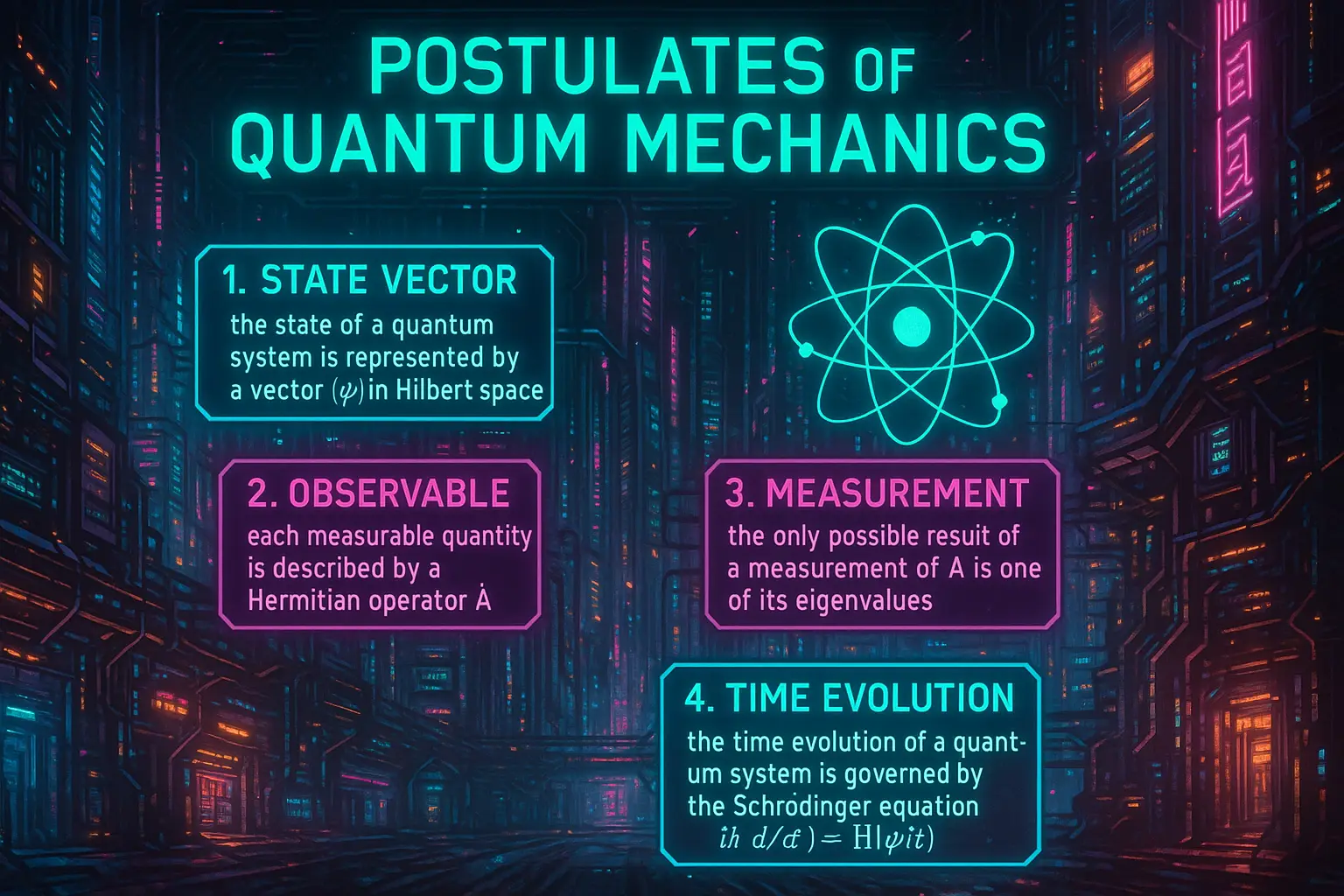
3. Postulate 1: State Vector and Hilbert Space

Every isolated physical system is described by a state vector \( |\psi\rangle \), which is an element of a Hilbert space \( \mathcal{H} \).

• The state encodes all measurable information about the system
• For composite systems, use tensor product of subsystems
• The state is normalized:
  \[
  \langle \psi | \psi \rangle = 1
  \]

Examples:

• Position basis: \( \psi(x) = \langle x | \psi \rangle \)
• Spin basis: \( |\psi\rangle = \alpha | \uparrow \rangle + \beta | \downarrow \rangle \)

4. Postulate 2: Observables and Operators

Every observable (measurable quantity) corresponds to a Hermitian operator \( \hat{A} \) acting on the Hilbert space.

• Measurement outcomes are eigenvalues of \( \hat{A} \):
  \[
  \hat{A} |a\rangle = a |a\rangle
  \]
• Hermitian operators have:
• Real eigenvalues
• Orthonormal eigenvectors
• Complete basis set

Examples:

• Position: \( \hat{x} \), Momentum: \( \hat{p} = -i\hbar \frac{d}{dx} \)

5. Postulate 3: Measurement and Expectation Values

The probability of obtaining result \( a \) from measuring \( \hat{A} \) in state \( |\psi\rangle \) is:

\[
P(a) = |\langle a | \psi \rangle|^2
\]

The expectation value of \( \hat{A} \) is:

\[
\langle \hat{A} \rangle = \langle \psi | \hat{A} | \psi \rangle
\]

Measurement alters the state — this is fundamentally different from classical physics.

6. Postulate 4: Time Evolution and Schrödinger Equation

Time evolution of a quantum state is deterministic and governed by the Schrödinger equation:

\[
i\hbar \frac{\partial}{\partial t} |\psi(t)\rangle = \hat{H} |\psi(t)\rangle
\]

Where:

• \( \hat{H} \) is the Hamiltonian (total energy operator)
• Solution:
  \[
  |\psi(t)\rangle = e^{-i\hat{H}t/\hbar} |\psi(0)\rangle
  \]

7. Postulate 5: Collapse of the Wavefunction

Upon measurement, the system collapses into one of the eigenstates of the measured observable.

• If \( a \) is observed, then immediately after:
  \[
  |\psi\rangle \rightarrow |a\rangle
  \]
• Collapse is instantaneous and probabilistic

This postulate introduces non-unitarity and is at the heart of interpretational debates.

8. Postulate 6: Identical Particles and Symmetrization

Particles are either:

• Bosons: symmetric under exchange
• Fermions: antisymmetric under exchange

Wavefunctions for identical particles must satisfy:

\[
\psi(x_1, x_2) = \pm \psi(x_2, x_1)
\]

• Fermions obey Pauli exclusion principle
• Bosons can occupy the same state (Bose–Einstein condensation)

9. Mathematical Framework and Examples

Example: Quantum harmonic oscillator

• Hamiltonian: \( \hat{H} = \frac{1}{2m} \hat{p}^2 + \frac{1}{2} m \omega^2 \hat{x}^2 \)
• Energy levels:
  \[
  E_n = \hbar \omega \left(n + \frac{1}{2}\right)
  \]

Example: Spin-1/2 system

• Basis: \( |\uparrow\rangle, |\downarrow\rangle \)
• Pauli matrices: \( \hat{\sigma}_x, \hat{\sigma}_y, \hat{\sigma}_z \)

10. Compatibility and Commutation Relations

Two observables \( \hat{A} \) and \( \hat{B} \) are compatible if they commute:

\[
[\hat{A}, \hat{B}] = 0
\]

• Compatible observables can be simultaneously measured
• Incompatible observables obey uncertainty relations

11. Uncertainty Principle from Postulates

From the non-commutativity of \( \hat{x} \) and \( \hat{p} \):

\[
[\hat{x}, \hat{p}] = i\hbar
\]

This leads to the Heisenberg uncertainty principle:

\[
\Delta x \Delta p \ge \frac{\hbar}{2}
\]

Limits precision of simultaneous measurements.

12. Relation to Classical Mechanics

Quantum mechanics recovers classical physics in the correspondence limit:

• Large quantum numbers \( n \rightarrow \infty \)
• \(\hbar \rightarrow 0\)
• Expectation values evolve classically (Ehrenfest’s theorem)

13. Role in Quantum Computing and Information

• Qubits are represented by state vectors in a two-dimensional Hilbert space
• Quantum gates are unitary operators
• Measurement collapses qubits probabilistically
• Postulates underpin quantum algorithms, entanglement, and teleportation

14. Interpretational Challenges

• What triggers wavefunction collapse?
• Is measurement observer-dependent?
• Realism vs probabilism vs many-worlds
• Are the postulates fundamental or emergent from deeper theory?

Debates continue in the foundations of quantum theory.

15. Conclusion

The postulates of quantum mechanics provide a rigorous framework that has successfully explained phenomena from atomic spectra to quantum entanglement. While complete in predictive power, they challenge our notions of reality, determinism, and causality — marking a profound departure from classical intuition. Mastery of these principles is the gateway to understanding the quantum world.