Table of Contents
- Introduction to Quantum Monte Carlo
- Monte Carlo Methods: A Primer
- The Quantum Many-Body Problem
- Core Quantum Monte Carlo Techniques
- Variational Monte Carlo (VMC)
- Diffusion Monte Carlo (DMC)
- Path Integral Monte Carlo (PIMC)
- Auxiliary Field Quantum Monte Carlo (AFQMC)
- The Fermion Sign Problem
- Practical Applications of Quantum Monte Carlo
- Condensed Matter Physics
- Quantum Chemistry
- Nuclear Physics
- Lattice Quantum Field Theory
- Computational Challenges and Strategies
- Future of QMC and Emerging Frontiers
- Conclusion
1. Introduction to Quantum Monte Carlo
Quantum Monte Carlo (QMC) is a suite of numerical methods designed to solve quantum mechanical problems using stochastic (randomized) algorithms. As quantum systems grow in complexity—such as many-electron atoms, interacting spins on a lattice, or superconducting materials—exact solutions become computationally infeasible due to exponential growth in the state space. QMC offers a powerful workaround by simulating these systems probabilistically, often producing results with very high accuracy.
While QMC methods vary in formulation and use case, they all share a core strategy: leveraging random sampling to estimate properties of quantum systems. Over time, QMC has become one of the most trusted computational tools in quantum chemistry, condensed matter physics, and quantum field theory.
2. Monte Carlo Methods: A Primer
Before diving into quantum-specific applications, it’s essential to understand Monte Carlo (MC) methods in general. MC methods estimate numerical quantities by using random samples to approximate integrals or solutions to mathematical problems. They’re widely used in finance, physics, statistics, and computer science.
Example:
To estimate the integral of a function f(x) from a to b, MC methods randomly sample points within the interval and average the function values at these points.
Formula:
In the quantum realm, integrals over configuration space, which are often high-dimensional and complex, are similarly approximated using random walks or importance sampling.
3. The Quantum Many-Body Problem
Quantum systems involving multiple particles (electrons, nucleons, etc.) are described by wavefunctions that depend on the coordinates and spins of all particles. For an N-particle system, the wavefunction resides in a 3N-dimensional space (or 4N including spin).
Solving the Schrödinger equation directly for these systems is usually intractable:
where H^ is the Hamiltonian operator.
Classical computers struggle with the exponential scaling of quantum state space, which makes QMC’s stochastic approach particularly appealing.
4. Core Quantum Monte Carlo Techniques
4.1 Variational Monte Carlo (VMC)
VMC is the most intuitive and straightforward QMC method. It starts with a trial wavefunction 
The central idea is to estimate the ground-state energy as:
Using importance sampling, points in configuration space are sampled with a probability distribution 
Key Strengths:
- Simplicity
- Easily parallelizable
- Can be used for optimization
Limitations:
- Depends on the quality of the trial wavefunction
- Rarely yields exact ground states
4.2 Diffusion Monte Carlo (DMC)
DMC improves upon VMC by using a projection technique. The wavefunction is evolved in imaginary time to project out the ground state:
This evolution filters out higher-energy states exponentially faster, leaving the ground state in the long-time limit.
The algorithm mimics this evolution via a random walk process combined with branching (weighting and replication of walkers). It is particularly successful in obtaining highly accurate ground-state energies.
Key Strengths:
- High precision
- Applicable to both bosons and fermions (with caveats)
Limitations:
- The fermion sign problem
- Relies on the fixed-node approximation for fermions
- Computationally expensive
4.3 Path Integral Monte Carlo (PIMC)
PIMC uses Feynman’s path integral formulation to model quantum particles as a collection of classical paths in imaginary time. This is particularly effective for simulating finite-temperature systems.
Each quantum particle becomes a polymer-like object, and their interactions are modeled via path integrals. The method is highly accurate for bosonic systems.
Applications:
- Superfluid helium
- Quantum dots
- Bose-Einstein condensates
Limitations:
- Severely limited by the sign problem for fermions
- Large memory requirements
4.4 Auxiliary Field Quantum Monte Carlo (AFQMC)
AFQMC transforms two-body interactions into integrals over auxiliary fields using a Hubbard-Stratonovich transformation. The original interacting system becomes a non-interacting system in fluctuating external fields.
This method is used in:
- Lattice models like the Hubbard model
- Quantum chemistry for correlated electrons
AFQMC is more flexible and scalable than DMC in some cases, though it also struggles with the sign problem.
5. The Fermion Sign Problem
Perhaps the greatest challenge in QMC for fermionic systems is the sign problem. Because fermionic wavefunctions are antisymmetric, some configurations contribute negatively to the expectation value.
In practice, this leads to cancellations that cause exponential growth in the variance of the simulation:
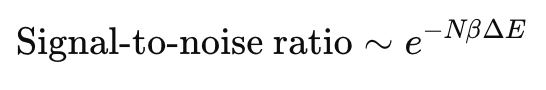
where N is the number of particles, β is inverse temperature, and ΔE is the energy gap.
Workarounds:
- Fixed-node approximation in DMC
- Constrained path approximation in AFQMC
- Symmetry restrictions to minimize negative weights
Despite progress, a general solution to the sign problem remains elusive and is an area of active research.
6. Practical Applications of Quantum Monte Carlo
6.1 Condensed Matter Physics
QMC plays a central role in studying electron correlation effects in materials, especially where density functional theory (DFT) fails.
- Magnetic properties of spin systems
- High-temperature superconductors
- Phase transitions in quantum lattices
- Quantum spin liquids
6.2 Quantum Chemistry
In quantum chemistry, QMC methods offer accuracy that rivals or surpasses coupled-cluster techniques, especially for:
- Molecular binding energies
- Reaction barriers
- Excited states (to a limited extent)
Software packages like QMCPACK and CASINO are designed specifically for molecular simulations using QMC.
6.3 Nuclear Physics
QMC is also used to solve nuclear Hamiltonians with realistic nucleon-nucleon interactions. Techniques like GFMC (Green’s Function Monte Carlo) are adapted for nuclei.
6.4 Lattice Quantum Field Theory
In lattice QCD and other quantum field theories, QMC enables non-perturbative simulations of gauge theories. This has been instrumental in:
- Computing hadron masses
- Investigating quark confinement
- Exploring phase transitions in quantum chromodynamics
7. Computational Challenges and Strategies
Despite its strengths, QMC has a steep computational cost, especially for systems with:
- Many interacting particles
- Fermionic statistics
- High-accuracy demands
Strategies to Mitigate Challenges:
- Importance sampling: Reduces variance by focusing on high-probability regions.
- Parallelization: QMC is highly parallelizable and scales well on supercomputers.
- Machine Learning: Deep neural networks (e.g., FermiNet, PauliNet) are now being integrated to represent wavefunctions more effectively.
- GPU Acceleration: Hardware acceleration has significantly reduced simulation time.
8. Future of QMC and Emerging Frontiers
QMC continues to evolve in step with advancements in computing and algorithmic innovation.
Emerging Areas:
- Quantum computing-assisted QMC: Using quantum devices to handle sign-problem-prone parts of the simulation.
- Neural network wavefunctions: Representing many-body wavefunctions using variational neural networks.
- Hybrid QMC-DFT methods: Combining the scalability of DFT with the accuracy of QMC.
The field is ripe for interdisciplinary collaboration—spanning physics, computer science, and applied mathematics.
9. Conclusion
Quantum Monte Carlo stands at the frontier of computational quantum mechanics, providing some of the most accurate tools for modeling many-body quantum systems. Despite limitations like the fermion sign problem and high computational demands, QMC methods have proven their worth across physics and chemistry.
As quantum systems become increasingly central to next-generation technologies—quantum computing, novel materials, and molecular design—QMC will likely grow in relevance, fueled by both algorithmic breakthroughs and advances in computational hardware.
Whether you’re a physicist aiming to understand superconductivity, a chemist optimizing molecular geometries, or a computer scientist building quantum-enhanced algorithms, Quantum Monte Carlo offers a versatile and profound toolkit for probing the quantum world.
