Table of Contents
- Introduction
- What Is a Quantum Non-Demolition (QND) Measurement?
- Motivation and Applications
- Quantum Measurement Backaction
- Conditions for QND Measurements
- Commutativity and Conserved Observables
- QND vs Projective and Weak Measurements
- QND Hamiltonian Interactions
- Example: Photon Number QND Measurement
- Example: QND of Atomic Population
- Gravitational Wave Detection and QND
- QND in Cavity QED and Circuit QED
- QND with Optomechanical Systems
- Measurement of Quantum Jumps
- Role in Quantum Error Correction
- Quantum State Preparation via QND
- Measurement-Based Quantum Feedback
- Challenges and Limitations
- Experimental Realizations
- Conclusion
1. Introduction
Quantum non-demolition (QND) measurements allow the extraction of information about a quantum system without altering the observable being measured. They provide a way to monitor quantum systems repeatedly and precisely without collapse-induced destruction of the state.
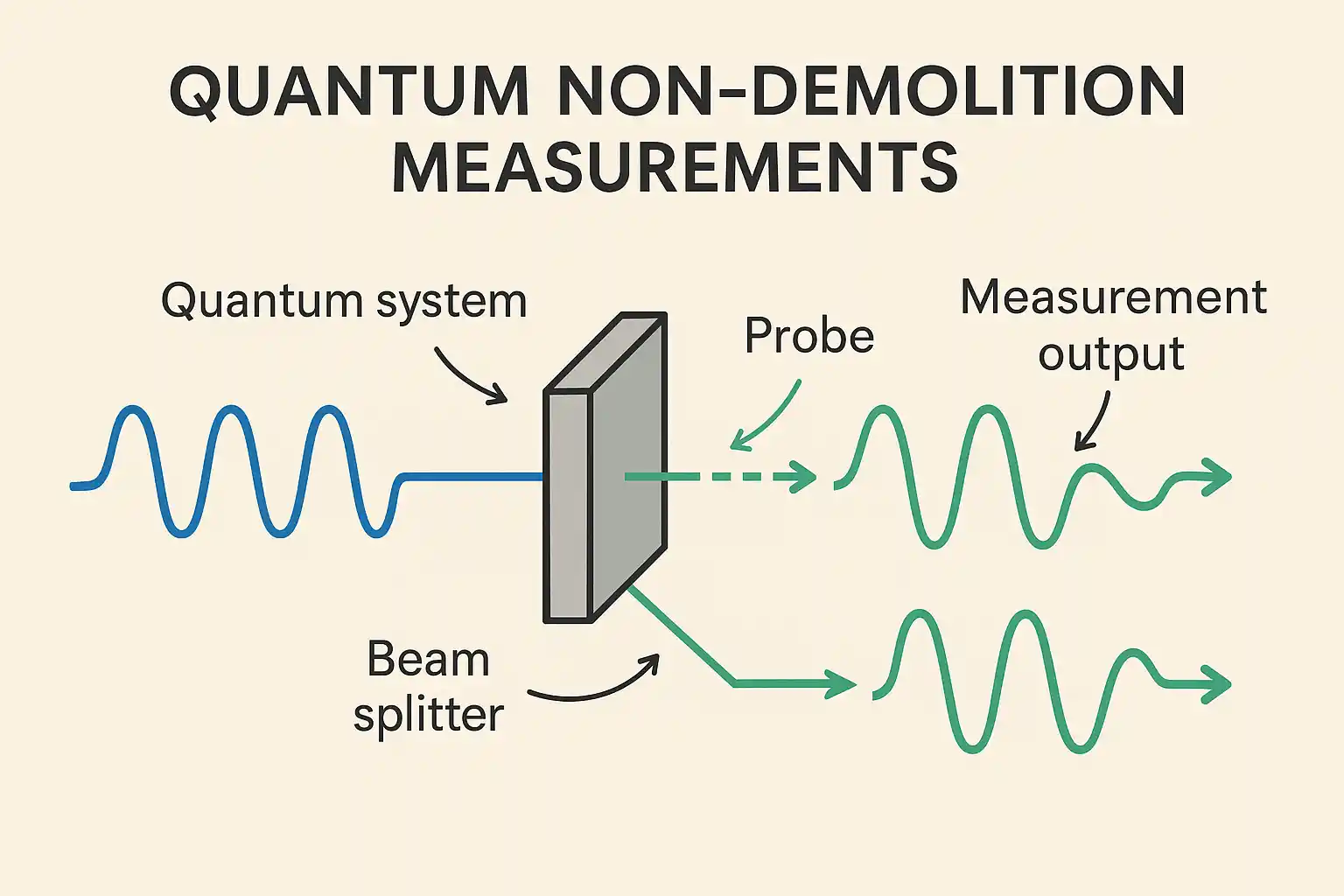
2. What Is a Quantum Non-Demolition (QND) Measurement?
A QND measurement determines the value of an observable while preserving its future measurability. Repeated measurements yield the same outcome, indicating that the observable is unaffected by the act of measurement.
3. Motivation and Applications
- Monitor quantum systems continuously
- Prepare and stabilize quantum states
- Enable quantum feedback and control
- Support quantum error correction protocols
- Essential in high-precision and low-noise measurements
4. Quantum Measurement Backaction
Standard quantum measurements perturb the system due to backaction. In QND, the observable commutes with the system’s Hamiltonian and the measurement operator, eliminating such disturbance.
5. Conditions for QND Measurements
- The observable \( \hat{O} \) must commute with the system Hamiltonian:
\[
[\hat{H}, \hat{O}] = 0
\] - The interaction Hamiltonian must couple the system to the probe without disturbing \( \hat{O} \).
6. Commutativity and Conserved Observables
If \( \hat{O} \) is a conserved quantity (\( [\hat{O}, H] = 0 \)), its value remains unchanged over time. Measuring such observables does not collapse the state destructively, satisfying QND conditions.
7. QND vs Projective and Weak Measurements
| Type | Collapse | Repeatability | System Disturbance |
|---|---|---|---|
| Projective | Yes | No | High |
| Weak | No | Limited | Minimal |
| QND | Yes/No | Yes | Minimal (on observable) |
8. QND Hamiltonian Interactions
A typical interaction Hamiltonian is:
\[
H_{ ext{int}} = \hbar g \hat{O} \otimes \hat{P}
\]
where \( \hat{O} \) is the system observable and \( \hat{P} \) is the conjugate observable of the measurement apparatus (probe).
9. Example: Photon Number QND Measurement
In cavity QED, atoms interact dispersively with a cavity. The phase shift in atomic levels reveals the number of photons \( n \) without absorbing them, leaving the photon number unchanged.
10. Example: QND of Atomic Population
In atomic ensembles, measuring population differences via Faraday rotation of probe light enables QND of spin projection, crucial for spin squeezing and quantum memory.
11. Gravitational Wave Detection and QND
QND techniques are proposed to overcome quantum limits in interferometric gravitational wave detectors (LIGO). They suppress backaction from radiation pressure noise.
12. QND in Cavity QED and Circuit QED
- In cavity QED: Non-destructive readout of photon numbers
- In circuit QED: Qubit state measured via dispersive shift of cavity frequency, preserving coherence of non-measured degrees of freedom
13. QND with Optomechanical Systems
QND of mechanical displacement or energy levels is achieved via radiation pressure interaction between light and moving mirrors in optical cavities.
14. Measurement of Quantum Jumps
QND enables observation of quantum jumps between energy levels in real time, revealing discrete nature of quantum state evolution.
15. Role in Quantum Error Correction
QND syndrome extraction allows detection of errors without destroying the encoded quantum information, essential for fault-tolerant quantum computing.
16. Quantum State Preparation via QND
Repeated QND measurements conditionally project the system into desired eigenstates, facilitating quantum state engineering and purification.
17. Measurement-Based Quantum Feedback
QND enables real-time monitoring and adaptive feedback to stabilize quantum systems or implement error-corrective control protocols.
18. Challenges and Limitations
- Technical noise and decoherence
- Imperfect isolation from other observables
- Implementation of true non-demolition interactions in large systems
19. Experimental Realizations
QND has been realized in:
- Microwave cavities with Rydberg atoms
- Circuit QED with superconducting qubits
- Atomic ensembles and squeezed light
- Optomechanical systems and cold atoms
20. Conclusion
Quantum non-demolition measurements provide a vital tool for quantum control, sensing, and information processing. By enabling repeated, non-invasive observation, they push the boundaries of measurement precision and quantum system manipulation.