Table of Contents
- Introduction
- Central Potentials and Radial Schrödinger Equation
- Separation of Variables in Spherical Coordinates
- Angular Momentum and the Centrifugal Term
- Redefining the Radial Equation
- Effective Potential and Physical Interpretation
- Principal Quantum Number \( n \)
- Orbital Angular Momentum Quantum Number \( \ell \)
- Radial Nodes and Quantum Number Relationships
- Solving the Radial Equation for Hydrogen
- Radial Wavefunctions and Laguerre Polynomials
- Bohr Radius and Atomic Length Scales
- Radial Probability Density
- Quantum Numbers and Degeneracy
- Extensions to Multi-Electron Atoms
- Conclusion
1. Introduction
In atomic quantum mechanics, understanding how the electron behaves within a central potential is key to predicting its energy levels and spatial distribution. The radial equation, derived from the 3D Schrödinger equation, contains essential physics and introduces important quantum numbers that govern atomic structure.
2. Central Potentials and Radial Schrödinger Equation
A central potential depends only on the distance from the origin:
\[
V(\vec{r}) = V(r)
\]
This symmetry allows the use of spherical coordinates \((r, \theta, \phi)\), leading to separable solutions and well-defined angular momentum properties.
3. Separation of Variables in Spherical Coordinates
Assume a total wavefunction:
\[
\psi(r, \theta, \phi) = R(r) Y(\theta, \phi)
\]
Substituting into the time-independent Schrödinger equation and separating variables yields:
- An angular equation, solved by spherical harmonics \( Y_\ell^m(\theta, \phi) \)
- A radial equation, which governs the energy and radial probability
4. Angular Momentum and the Centrifugal Term
From the angular solution, we get:
\[
\hat{L}^2 Y_\ell^m = \hbar^2 \ell(\ell+1) Y_\ell^m
\]
This leads to a term in the radial equation:
\[
\frac{\ell(\ell+1)\hbar^2}{2\mu r^2}
\]
Called the centrifugal barrier, it prevents low-\( \ell \) states from collapsing at the origin and shapes the effective potential.
5. Redefining the Radial Equation
Define a new function \( u(r) = r R(r) \). The radial equation becomes:
\[
\frac{d^2 u}{dr^2} + \left[ \frac{2\mu}{\hbar^2}(E – V(r)) – \frac{\ell(\ell+1)}{r^2} \right] u(r) = 0
\]
This is a second-order differential equation whose solutions provide the allowed radial wavefunctions and energy levels.
6. Effective Potential and Physical Interpretation
Rewriting the radial equation:
\[
\frac{d^2 u}{dr^2} + \frac{2\mu}{\hbar^2} \left[E – V_{\text{eff}}(r) \right] u(r) = 0
\]
Where:
\[
V_{\text{eff}}(r) = V(r) + \frac{\hbar^2 \ell(\ell+1)}{2\mu r^2}
\]
- The second term acts like a repulsive force
- Influences the turning points and radial confinement
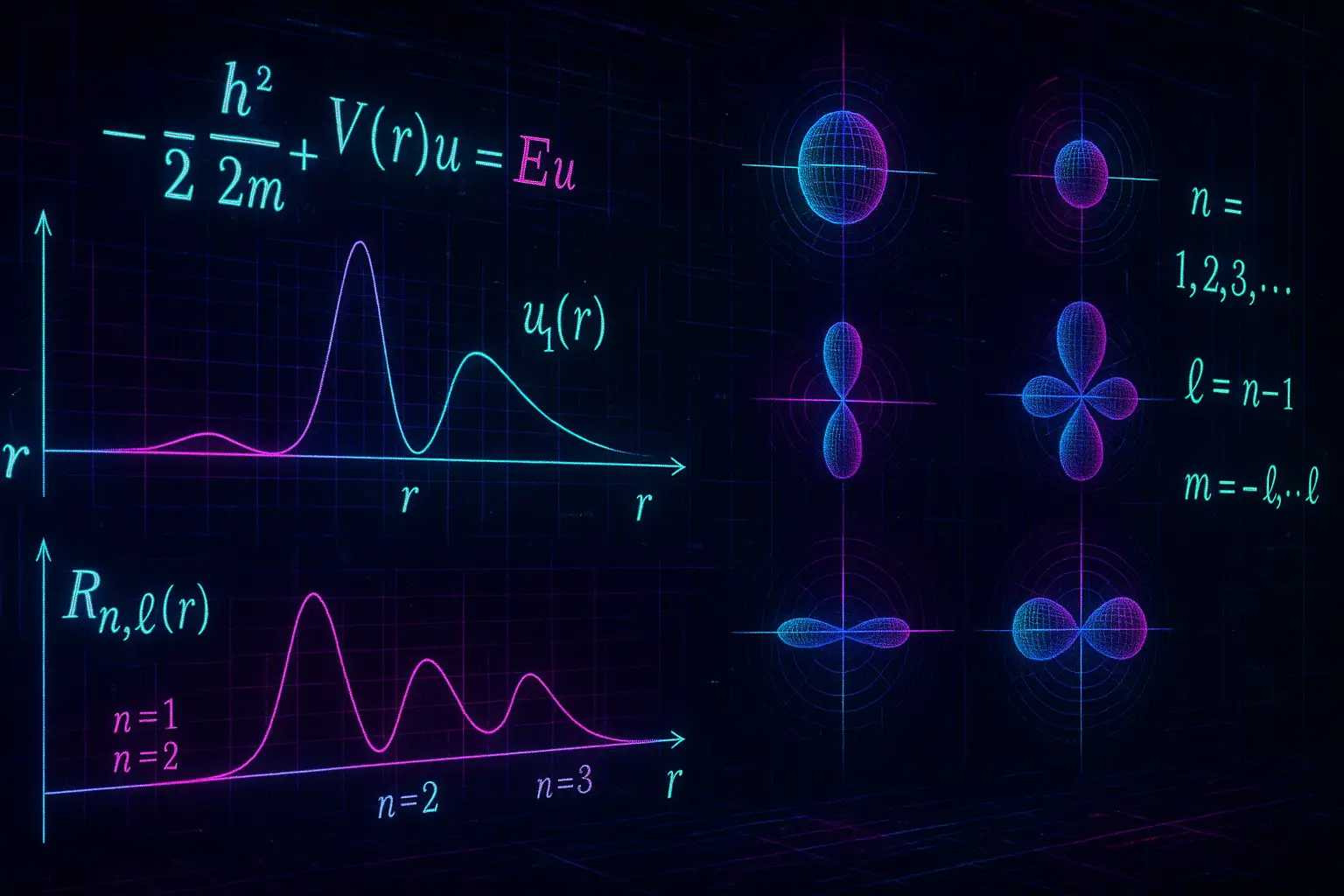
7. Principal Quantum Number \( n \)
The principal quantum number \( n \) labels energy levels:
\[
n = 1, 2, 3, \dots
\]
It arises from boundary conditions ensuring normalizable and finite solutions. In hydrogen-like atoms:
\[
E_n = -\frac{\mu e^4}{2(4\pi\varepsilon_0)^2 \hbar^2 n^2}
\]
8. Orbital Angular Momentum Quantum Number \( \ell \)
The quantum number \( \ell \) arises from solving the angular equation:
- Determines the shape of the orbital
- Allowed values: \( \ell = 0, 1, 2, \dots, n-1 \)
It also appears in the centrifugal term, shaping the radial solution.
9. Radial Nodes and Quantum Number Relationships
The number of radial nodes \( n_r \) (zero crossings in \( R(r) \)) is:
\[
n_r = n – \ell – 1
\]
Thus:
- Ground state (\( n = 1, \ell = 0 \)): 0 nodes
- Higher \( n \): more nodes, more oscillatory behavior
10. Solving the Radial Equation for Hydrogen
For hydrogen’s Coulomb potential:
\[
V(r) = -\frac{e^2}{4\pi\varepsilon_0 r}
\]
The radial solutions involve associated Laguerre polynomials:
\[
R_{n\ell}(r) = \rho^\ell e^{-\rho/2} L_{n – \ell – 1}^{2\ell + 1}(\rho), \quad \rho = \frac{2r}{n a_0}
\]
Where \( a_0 \) is the Bohr radius.
11. Radial Wavefunctions and Laguerre Polynomials
Radial functions are:
\[
R_{n\ell}(r) = N_{n\ell} \left( \frac{r}{a_0} \right)^\ell e^{-r/(na_0)} L_{n-\ell-1}^{2\ell+1} \left( \frac{2r}{na_0} \right)
\]
These are orthogonal and form a complete basis for bound states.
12. Bohr Radius and Atomic Length Scales
The Bohr radius is:
\[
a_0 = \frac{4\pi \varepsilon_0 \hbar^2}{\mu e^2}
\]
It defines the natural length scale of hydrogenic orbitals.
Typical orbital sizes increase with \( n \), as \( \langle r \rangle \sim n^2 a_0 \).
13. Radial Probability Density
The radial probability density is:
\[
P(r) = |R(r)|^2 r^2
\]
Gives the likelihood of finding the electron at a distance \( r \). Plots of \( P(r) \) show peaks and nodes, visualizing electron shell structure.
14. Quantum Numbers and Degeneracy
Each energy level \( n \) has a degeneracy of:
\[
g_n = n^2 = \sum_{\ell=0}^{n-1} (2\ell + 1)
\]
This reflects the number of allowed \( \ell \) and \( m \) values per \( n \).
15. Extensions to Multi-Electron Atoms
While hydrogen allows exact solutions, in multi-electron atoms:
- The radial equation is modified by electron shielding
- \( n \) and \( \ell \) remain, but energies depend on screened nuclear charge
- Leads to fine structure splitting and shell structures
16. Conclusion
The radial equation lies at the heart of quantum atomic theory. It introduces key quantum numbers that define the structure, energy, and behavior of atomic orbitals. Understanding how radial functions and quantum numbers interplay provides a deeper insight into electron configuration, spectroscopy, and the periodic table.