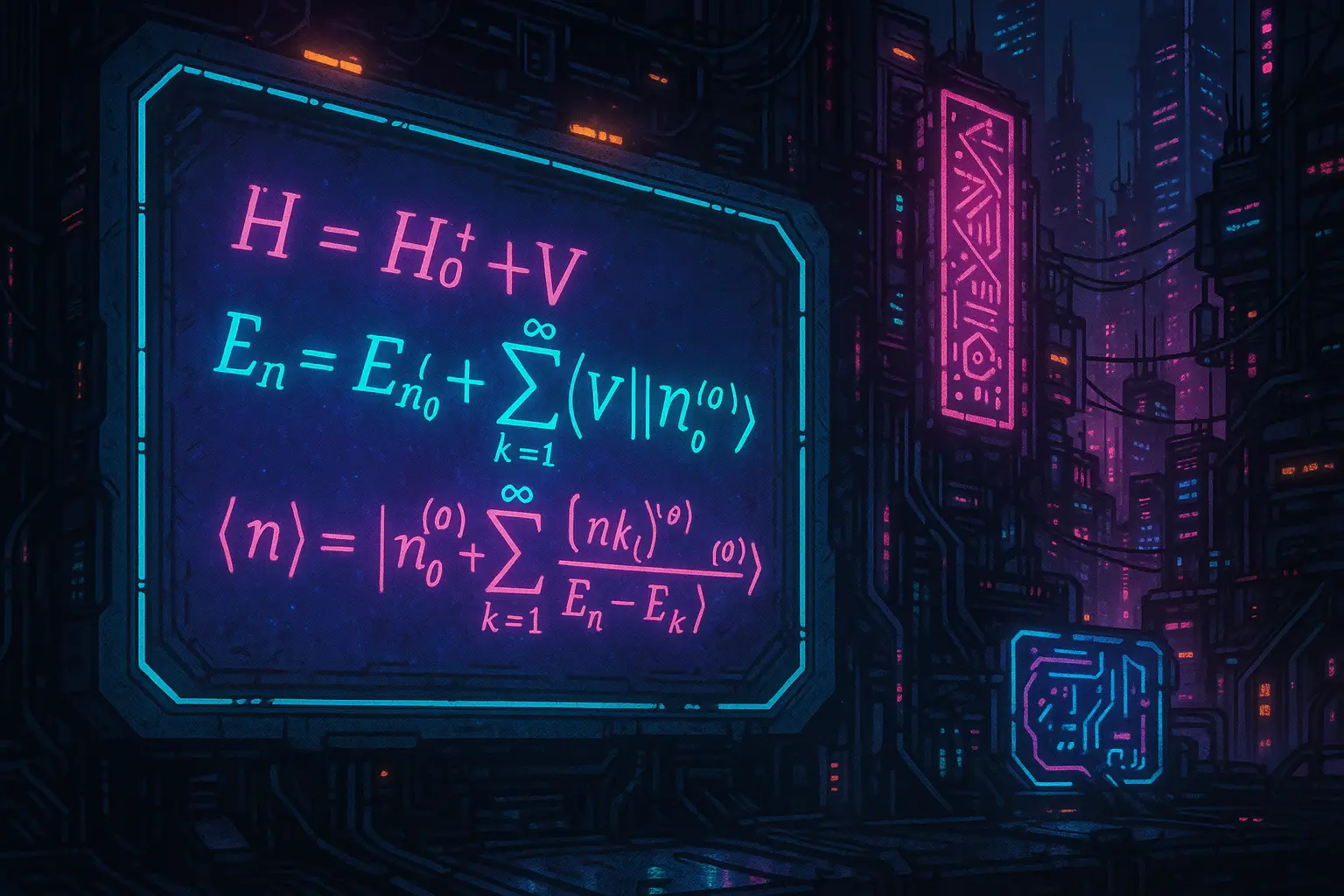Table of Contents
- Introduction
- Motivation for Perturbation Theory
- The General Setup
- Unperturbed and Perturbed Hamiltonians
- Expansion of Energy and Wavefunctions
- First-Order Corrections to Energy
- First-Order Corrections to Wavefunctions
- Second-Order Corrections to Energy
- Degenerate Perturbation Theory
- Example: Non-Degenerate Perturbation in 1D Harmonic Oscillator
- Example: Degenerate Perturbation in the Hydrogen Atom
- Applications of Time-Independent Perturbation Theory
- Limitations of the Method
- Variants and Extensions
- Conclusion
1. Introduction
Perturbation theory is a powerful approximation technique in quantum mechanics that allows us to find approximate solutions to problems that cannot be solved exactly. In many physical systems, the Hamiltonian can be written as a sum of a solvable part and a small perturbing term. Time-independent perturbation theory applies when the perturbation does not vary with time.
2. Motivation for Perturbation Theory
- Exact solutions are known only for a few systems (e.g., hydrogen atom, harmonic oscillator).
- Most realistic systems involve additional terms or interactions not present in the solvable version.
- Perturbation theory gives a way to expand around a known solution and include small corrections.
3. The General Setup
Suppose the full Hamiltonian is:
\[
\hat{H} = \hat{H}_0 + \lambda \hat{H}’
\]
Where:
- \( \hat{H}_0 \): unperturbed Hamiltonian with known eigenstates and eigenvalues.
- \( \hat{H}’ \): perturbing Hamiltonian.
- \( \lambda \): bookkeeping parameter (set to 1 at the end).
We seek the eigenvalues and eigenstates of \( \hat{H} \) in a power series expansion.
4. Unperturbed and Perturbed Hamiltonians
Let:
\[
\hat{H}_0 |\psi_n^{(0)}\rangle = E_n^{(0)} |\psi_n^{(0)}\rangle
\]
Then the true energy and wavefunction are expanded as:
\[
E_n = E_n^{(0)} + \lambda E_n^{(1)} + \lambda^2 E_n^{(2)} + \dots
\]
\[
|\psi_n\rangle = |\psi_n^{(0)}\rangle + \lambda |\psi_n^{(1)}\rangle + \lambda^2 |\psi_n^{(2)}\rangle + \dots
\]
5. Expansion of Energy and Wavefunctions
Substitute the expansions into the Schrödinger equation and match powers of \( \lambda \):
\[
(\hat{H}_0 + \lambda \hat{H}’)(|\psi_n^{(0)}\rangle + \lambda |\psi_n^{(1)}\rangle + \dots) = (E_n^{(0)} + \lambda E_n^{(1)} + \dots)(|\psi_n^{(0)}\rangle + \lambda |\psi_n^{(1)}\rangle + \dots)
\]
6. First-Order Corrections to Energy
The first-order energy correction is:
\[
E_n^{(1)} = \langle \psi_n^{(0)} | \hat{H}’ | \psi_n^{(0)} \rangle
\]
This is the expectation value of the perturbation in the unperturbed state.
7. First-Order Corrections to Wavefunctions
The first-order wavefunction correction is:
\[
|\psi_n^{(1)}\rangle = \sum_{k \ne n} \frac{\langle \psi_k^{(0)} | \hat{H}’ | \psi_n^{(0)} \rangle}{E_n^{(0)} – E_k^{(0)}} |\psi_k^{(0)}\rangle
\]
Only states different from \( n \) contribute.
8. Second-Order Corrections to Energy
The second-order correction is:
\[
E_n^{(2)} = \sum_{k \ne n} \frac{|\langle \psi_k^{(0)} | \hat{H}’ | \psi_n^{(0)} \rangle|^2}{E_n^{(0)} – E_k^{(0)}}
\]
This gives information on how much the other states influence the perturbed energy level.
9. Degenerate Perturbation Theory
When \( \hat{H}_0 \) has degenerate eigenstates, the standard method fails because denominators vanish. In this case:
- Diagonalize \( \hat{H}’ \) within the degenerate subspace.
- Construct new linear combinations of degenerate states that diagonalize the perturbation.
- Use these as the basis for applying perturbation theory.
10. Example: Non-Degenerate Perturbation in 1D Harmonic Oscillator
Let the perturbation be:
\[
\hat{H}’ = \alpha x^4
\]
This leads to shifts in energy levels that can be computed using the known oscillator eigenstates and matrix elements of \( x^4 \).
11. Example: Degenerate Perturbation in the Hydrogen Atom
In hydrogen:
- The degeneracy in \( \ell \) is lifted by a perturbation like the spin-orbit coupling.
- Degenerate perturbation theory helps to calculate fine structure corrections.
12. Applications of Time-Independent Perturbation Theory
- Fine structure in atoms
- Stark effect (electric field perturbation)
- Zeeman effect (magnetic field perturbation)
- Anharmonic oscillators in molecular vibrations
13. Limitations of the Method
- Assumes the perturbation is small.
- Diverges if energy levels are too close or perturbation is too strong.
- Not suitable for non-analytic or discontinuous perturbations.
14. Variants and Extensions
- Time-dependent perturbation theory for dynamics and transitions.
- Rayleigh–Schrödinger perturbation theory
- Brillouin–Wigner perturbation theory
15. Conclusion
Time-independent perturbation theory is a cornerstone of quantum approximation methods. It allows physicists to incorporate the effects of weak interactions and fields on known systems, and predict how energy levels and states shift in realistic environments. It bridges exact theory with experimental reality, enabling the study of a wide range of quantum systems.