Table of Contents

1. Introduction
2. Why Go Beyond Newton?
3. Generalized Coordinates
4. Principle of Least Action
5. The Lagrangian Function
6. Euler-Lagrange Equation
7. Simple Example: Free Particle
8. Simple Harmonic Oscillator in Lagrangian Formalism
9. Atwood Machine via Lagrangian
10. Constraints and Degrees of Freedom
11. Advantages of the Lagrangian Approach
12. Connection to Quantum Mechanics
13. Conclusion

---

1. Introduction

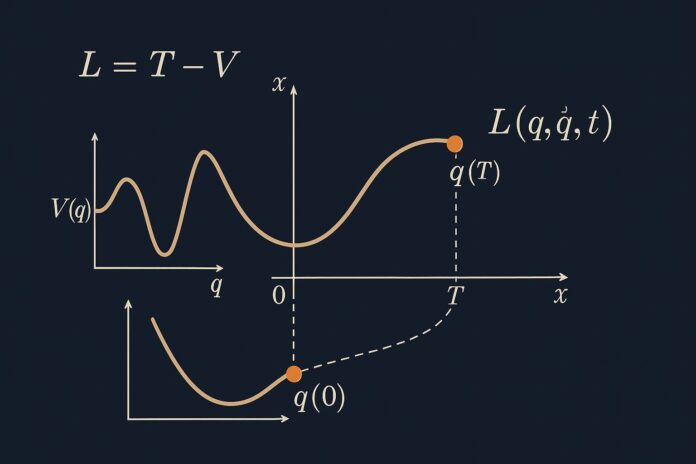
Lagrangian mechanics is an elegant and powerful reformulation of classical mechanics. Instead of focusing directly on forces (as Newtonian mechanics does), it builds from energy principles to describe the motion of systems. At its core is the idea that systems evolve in a way that minimizes (or extremizes) a quantity called action.

While Newton’s approach is intuitive and practical for many problems, the Lagrangian formulation excels in systems with constraints, symmetry, and complex interactions — making it invaluable for theoretical physics and quantum mechanics.

---

2. Why Go Beyond Newton?

Newton’s laws work well for many problems — pushing blocks, falling objects, or planetary motion. But when dealing with:

• Multiple degrees of freedom
• Non-Cartesian coordinates
• Complicated constraints
• Systems with symmetries (e.g., rotational)

Newton’s method becomes cumbersome. Lagrangian mechanics handles such cases more naturally by focusing on scalar quantities (energy) and minimizing action rather than computing forces directly.

---

3. Generalized Coordinates

In Lagrangian mechanics, we use generalized coordinates:

• Denoted by \( q_1, q_2, …, q_n \)
• Can be angles, distances, or any parameters describing the configuration of the system
• Useful in non-Cartesian systems like pendulums, rotating bodies, or spherical systems

Instead of dealing with vectors \( \vec{F} \), we describe the configuration of a system in terms of coordinates and velocities \( \dot{q}_i \).

---

4. Principle of Least Action

The foundation of Lagrangian mechanics is the Principle of Least Action.

It states:

A physical system evolves between two configurations such that the action integral is minimized (or extremized).

The action is defined as:

\[
S = \int_{t_1}^{t_2} L(q_i, \dot{q}_i, t) \, dt
\]

Where:

• \( L \) is the Lagrangian of the system
• \( q_i \) and \( \dot{q}_i \) are generalized coordinates and their velocities

This principle is powerful because it leads to equations of motion without invoking force vectors directly.

---

5. The Lagrangian Function

The Lagrangian is a function defined as:

\[
L = T – U
\]

Where:

• \( T \): kinetic energy
• \( U \): potential energy

It captures the dynamics of the system through energy differences, rather than forces.

Think of the Lagrangian as a measure of how much “freedom” the system has to move, given its energy configuration.

---

6. Euler-Lagrange Equation

The condition for minimizing the action leads to the Euler-Lagrange equations:

\[
\frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}_i} \right) – \frac{\partial L}{\partial q_i} = 0
\]

This is the core equation of motion in Lagrangian mechanics. It replaces \( F = ma \) with a more general and coordinate-independent formulation.

You derive one Euler-Lagrange equation for each generalized coordinate \( q_i \).

---

7. Simple Example: Free Particle

Let’s apply the Euler-Lagrange equation to a free particle (no potential energy):

• Kinetic energy: \( T = \frac{1}{2}m\dot{x}^2 \)
• Potential energy: \( U = 0 \)

So, the Lagrangian is:

\[
L = \frac{1}{2}m\dot{x}^2
\]

Using Euler-Lagrange:

\[
\frac{d}{dt} \left( m\dot{x} \right) = 0 \quad \Rightarrow \quad m\ddot{x} = 0
\]

This confirms Newton’s first law: a free particle moves at constant velocity.

---

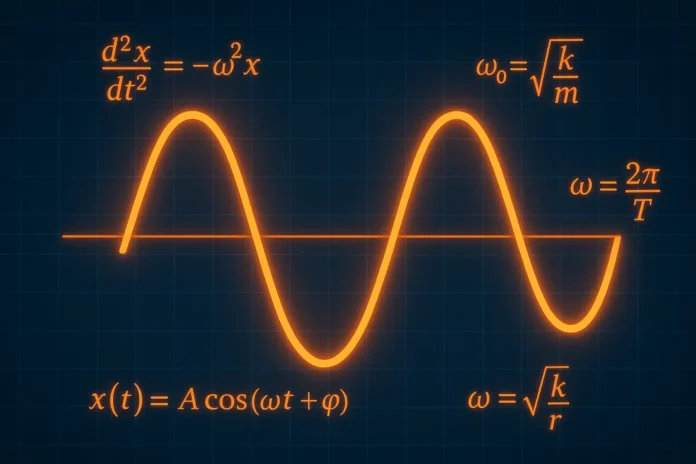
8. SHO in Lagrangian Formalism

Let’s re-derive the simple harmonic oscillator (spring system) using Lagrangian mechanics.

• \( T = \frac{1}{2}m\dot{x}^2 \)
• \( U = \frac{1}{2}kx^2 \)

\[
L = \frac{1}{2}m\dot{x}^2 – \frac{1}{2}kx^2
\]

Now apply the Euler-Lagrange equation:

\[
\frac{d}{dt}(m\dot{x}) + kx = 0 \Rightarrow m\ddot{x} + kx = 0
\]

This reproduces the SHO differential equation — but without invoking any forces explicitly.

---

9. Atwood Machine via Lagrangian

Consider an Atwood machine: two masses \( m_1 \) and \( m_2 \) connected by a string over a pulley.

Let \( x \) be the displacement of \( m_1 \) downward (so \( m_2 \) moves up by the same amount).

• \( T = \frac{1}{2}m_1 \dot{x}^2 + \frac{1}{2}m_2 \dot{x}^2 = \frac{1}{2}(m_1 + m_2)\dot{x}^2 \)
• \( U = -m_1gx + m_2g x = (m_2 – m_1)gx \)

Lagrangian:

\[
L = \frac{1}{2}(m_1 + m_2)\dot{x}^2 – (m_2 – m_1)gx
\]

Apply Euler-Lagrange:

\[
(m_1 + m_2)\ddot{x} = (m_2 – m_1)g
\]

Which matches the standard result obtained via Newton’s laws — but more elegantly.

---

10. Constraints and Degrees of Freedom

A major strength of the Lagrangian approach is its treatment of constraints.

• Constraints restrict motion (e.g., a pendulum is constrained to swing along an arc).
• Rather than using forces of constraint (like tension), Lagrangian mechanics handles them by reducing the number of coordinates.

The number of degrees of freedom equals the number of independent generalized coordinates after accounting for constraints.

---

11. Advantages of the Lagrangian Approach

• Coordinate-independence: Works in polar, spherical, or any coordinates.
• Scales well: Easily applies to multi-body systems.
• Energy-based: Uses scalar quantities (simpler math).
• Elegant with symmetries: Symmetries lead to conservation laws (via Noether’s theorem).
• Foundation for quantum mechanics and field theory.

---

12. Connection to Quantum Mechanics

Lagrangian mechanics leads directly into quantum physics via Feynman’s path integral formulation, where the probability of a particle’s path is weighted by:

\[
e^{iS/\hbar}
\]

The action \( S \) is the same as in classical mechanics:

\[
S = \int L \, dt
\]

In this view, all paths are possible, but the classical path is the one where the action is extremized — precisely the Principle of Least Action.

---

13. Conclusion

Lagrangian mechanics reimagines motion as an optimization problem, replacing Newton’s vector-based force laws with elegant energy principles. It’s especially powerful in dealing with complex systems, constraints, and arbitrary coordinates — and provides the conceptual bridge from classical physics to quantum mechanics.

For learners, mastering this framework not only simplifies many physical problems but also prepares the ground for understanding advanced physics — from quantum field theory to general relativity.

---

Table of Contents

1. Introduction
2. What Is an Oscillator?
3. The Simple Harmonic Oscillator (SHO)
4. Equation of Motion for SHO
5. Energy in Simple Harmonic Motion
6. Phase Space Representation
7. Damped Harmonic Oscillator
8. Driven Harmonic Oscillator
9. Resonance and Phase Lag
10. Nonlinear Oscillators (Overview)
11. Applications of Classical Oscillators
12. Transition to Quantum Oscillators
13. Conclusion

---

1. Introduction

Oscillatory systems are central to physics, engineering, and nature. Whether it’s a pendulum swinging, a mass on a spring, or the vibrations of atoms in a crystal, oscillations describe periodic motion fundamental to physical systems.

Classical oscillators are typically governed by Newton’s laws and offer an elegant example of how simple differential equations model physical reality. Understanding these systems builds the conceptual foundation for wave mechanics, circuit theory, molecular dynamics, and even quantum field theory.

---

2. What Is an Oscillator?

An oscillator is any system that exhibits periodic or quasi-periodic motion about an equilibrium point. The force driving the motion often arises from a restoring force, which increases with displacement from equilibrium and acts in the opposite direction.

Examples:

• Mass-spring system
• Simple pendulum (small angle)
• LC electrical circuits
• Vibrating strings

---

3. The Simple Harmonic Oscillator (SHO)

The simplest and most fundamental type of oscillator is the simple harmonic oscillator, where the restoring force is proportional to displacement:

\[
F = -kx
\]

Where:

• k is the spring constant,
• x is the displacement from equilibrium.

Using Newton’s second law \( F = ma \):

\[
m\ddot{x} + kx = 0
\]

This is the defining differential equation for SHO.

---

4. Equation of Motion for SHO

The general solution to the SHO differential equation:

\[
\ddot{x} + \omega^2 x = 0, \quad \text{where} \quad \omega = \sqrt{\frac{k}{m}}
\]

is given by:

\[
x(t) = A \cos(\omega t + \phi)
\]

Where:

• A is the amplitude,
• \(\phi\) is the phase constant,
• \(\omega\) is the angular frequency.

Velocity and acceleration:

\[
v(t) = -A\omega \sin(\omega t + \phi)
\]
\[
a(t) = -A\omega^2 \cos(\omega t + \phi)
\]

---

5. Energy in Simple Harmonic Motion

The SHO conserves mechanical energy (no damping or driving forces). The total energy is the sum of kinetic and potential energies:

• Kinetic Energy:
  \[
  K = \frac{1}{2}mv^2 = \frac{1}{2}mA^2 \omega^2 \sin^2(\omega t + \phi)
  \]
• Potential Energy:
  \[
  U = \frac{1}{2}kx^2 = \frac{1}{2}kA^2 \cos^2(\omega t + \phi)
  \]
• Total Energy:
  \[
  E = K + U = \frac{1}{2}kA^2 = \text{constant}
  \]

The energy oscillates between kinetic and potential forms.

---

6. Phase Space Representation

In phase space, SHO is represented as a circular or elliptical trajectory in the x – v plane.

\[
\left( \frac{x}{A} \right)^2 + \left( \frac{v}{A\omega} \right)^2 = 1
\]

This indicates conservation of energy and cyclical motion.

---

7. Damped Harmonic Oscillator

\[
m\ddot{x} + b\dot{x} + kx = 0
\]

Three regimes:

1. Underdamped (/( b^2 < 4mk /)):
   \[
   x(t) = A e^{-\gamma t} \cos(\omega’ t + \phi)
   \]
   where \( \gamma = \frac{b}{2m}, \ \omega’ = \sqrt{\omega^2 – \gamma^2} \)
2. Critically damped (\( b^2 = 4mk \))
3. Overdamped (\( b^2 > 4mk \))

---

8. Driven Harmonic Oscillator

An external periodic force drives the system:

\[
m\ddot{x} + b\dot{x} + kx = F_0 \cos(\omega_d t)
\]

This leads to a steady-state solution where the system oscillates at the driving frequency ωd\omega_dωd​:

\[
x(t) = A(\omega_d) \cos(\omega_d t + \delta)
\]

Where:

\[
A(\omega_d) = \frac{F_0/m}{\sqrt{(\omega_0^2 – \omega_d^2)^2 + (2\gamma\omega_d)^2}}
\]

and δ\deltaδ is the phase lag.

---

9. Resonance and Phase Lag

Resonance occurs when the driving frequency ωd\omega_dωd​ matches the natural frequency ω0\omega_0ω0​:

\[
\omega_d = \omega_0 = \sqrt{\frac{k}{m}}
\]

At resonance, the amplitude is maximized (especially in low damping):

\[
A_{\text{res}} = \frac{F_0}{b\omega_0}
\]

Phase lag:

• Below resonance: oscillator lags driver
• At resonance: phase difference = π2\frac{\pi}{2}2π​
• Above resonance: oscillator leads driver

---

10. Nonlinear Oscillators (Overview)

When the restoring force is not proportional to displacement, the system becomes nonlinear.

Example: Duffing oscillator

\[
m\ddot{x} + b\dot{x} + kx + \beta x^3 = 0
\]

Nonlinear oscillators can exhibit:

• Amplitude-dependent frequencies,
• Bifurcations,
• Chaos under certain conditions.

These systems are harder to solve analytically and are typically explored using numerical methods.

---

11. Applications of Classical Oscillators

Oscillatory systems appear in nearly every branch of science:

• Mechanics: Springs, pendulums, suspension systems.
• Electronics: LC and RLC circuits follow similar differential equations.
• Engineering: Resonance in bridges, damping in building structures.
• Biology: Heartbeats, circadian rhythms.
• Optics: Light interference and cavity oscillations.
• Acoustics: Sound wave production and propagation.

---

12. Transition to Quantum Oscillators

The quantum harmonic oscillator is one of the few analytically solvable systems in quantum mechanics.

It replaces Newton’s second law with the Schrödinger equation:

\[
-\frac{\hbar^2}{2m} \frac{d^2 \psi}{dx^2} + \frac{1}{2}kx^2 \psi = E \psi
\]

The solutions yield quantized energy levels:

\[
E_n = \left( n + \frac{1}{2} \right)\hbar \omega
\]

No classical oscillator has a non-zero ground-state energy — a key difference with quantum behavior.

---

13. Conclusion

Classical oscillators, especially the simple harmonic oscillator, serve as idealized systems for understanding periodic motion. Their mathematical tractability and wide applicability make them essential for studying more complex phenomena such as wave propagation, resonance, and quantum transitions.

From the swing of a pendulum to electron behavior in atoms, oscillators represent one of physics’ most universal and unifying models.