Table of Contents

1. Introduction
2. What Is Phase Space?
3. Coordinates in Phase Space
4. Trajectories and Hamiltonian Flow
5. Volume Elements and Liouville’s Theorem
6. What Is Symplectic Geometry?
7. The Symplectic Form
8. Canonical Transformations and Symplectic Structure
9. Poisson Brackets and Symplectic Geometry
10. Darboux’s Theorem
11. Symplectic Manifolds in Higher Dimensions
12. Applications in Physics
13. Conclusion

---

1. Introduction

Classical mechanics is often introduced in terms of position and velocity. But to fully capture the structure of dynamical systems — and transition smoothly to quantum mechanics — we need a more refined view. That’s where phase space and symplectic geometry come in.

These concepts allow us to treat motion geometrically. Instead of tracking a particle along a path in space, we follow its state in phase space, where all possible positions and momenta are mapped out.

Symplectic geometry provides the mathematical structure underlying this space — a geometry of areas, not distances.

---

2. What Is Phase Space?

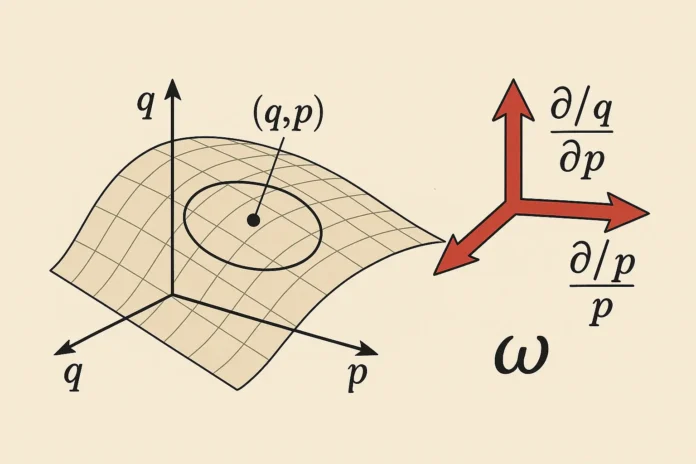
Phase space is a space where each point represents a complete state of a physical system.

For a system with \( n \) degrees of freedom:

• Position coordinates: \( q_1, q_2, …, q_n \)
• Momentum coordinates: \( p_1, p_2, …, p_n \)

The full state is a point in the \( 2n \)-dimensional phase space:

\[
\text{Phase space vector: } \mathbf{z} = (q_1, …, q_n, p_1, …, p_n)
\]

Each trajectory in phase space corresponds to the evolution of a system over time.

---

3. Coordinates in Phase Space

For a simple one-dimensional system:

• Position: \( q \)
• Momentum: \( p \)

The phase space is the \( (q, p) \)-plane. The evolution of the system is a curve in this plane.

In general, for \( n \) degrees of freedom, we need \( 2n \) coordinates.

---

4. Trajectories and Hamiltonian Flow

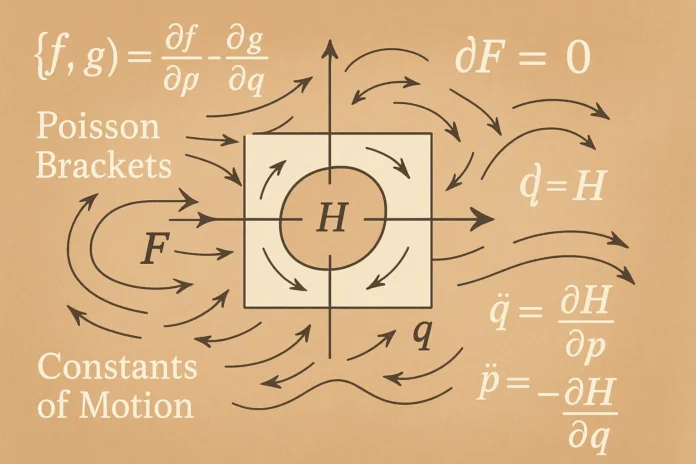
The motion in phase space is governed by Hamilton’s equations:

\[
\dot{q}_i = \frac{\partial H}{\partial p_i}, \quad \dot{p}_i = -\frac{\partial H}{\partial q_i}
\]

These define a vector field on phase space — the direction and speed at which the system evolves. A trajectory is an integral curve of this field.

---

5. Volume Elements and Liouville’s Theorem

In phase space, we can define a volume element:

\[
dV = dq_1 \wedge dp_1 \wedge \dots \wedge dq_n \wedge dp_n
\]

Liouville’s theorem states:

The volume in phase space is preserved under Hamiltonian flow.

This expresses conservation of information — the “density” of phase points does not change over time.

---

6. What Is Symplectic Geometry?

Symplectic geometry is a branch of differential geometry that focuses on the structure of phase space. It deals with non-degenerate, closed 2-forms, especially the symplectic form, which encodes the structure of classical mechanics.

Symplectic geometry is the natural setting for Hamiltonian dynamics.

---

7. The Symplectic Form

The canonical symplectic form in \( 2n \)-dimensional phase space is:

\[
\omega = \sum_{i=1}^n dq_i \wedge dp_i
\]

This form captures the geometry of the phase space. It is:

• Non-degenerate: Ensures invertibility between positions and momenta.
• Closed: \( d\omega = 0 \), which underpins conservation laws.

---

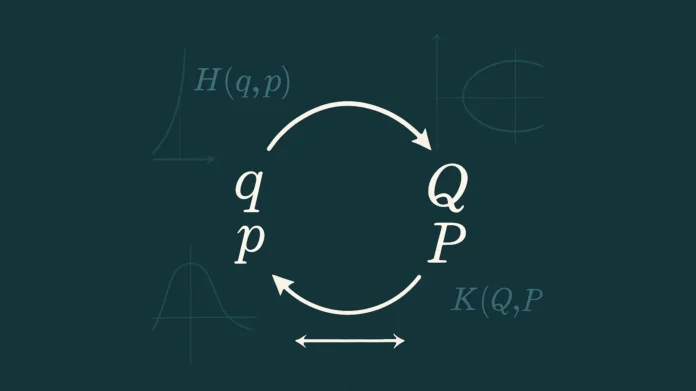
8. Canonical Transformations and Symplectic Structure

A canonical transformation is one that preserves the symplectic form:

\[
\omega’ = \omega
\]

This means the new coordinates still satisfy Hamilton’s equations and maintain the same physical content. Such transformations are also called symplectomorphisms.

---

9. Poisson Brackets and Symplectic Geometry

Poisson brackets arise naturally in symplectic geometry. For two functions \( f \) and \( g \), their Poisson bracket is:

\[
\{f, g\} = \sum_i \left( \frac{\partial f}{\partial q_i} \frac{\partial g}{\partial p_i} – \frac{\partial f}{\partial p_i} \frac{\partial g}{\partial q_i} \right)
\]

This is equivalent to:

\[
\{f, g\} = \omega(X_f, X_g)
\]

where \( X_f \) is the Hamiltonian vector field associated with \( f \). This shows that Poisson brackets are rooted in the geometry of symplectic space.

---

10. Darboux’s Theorem

A powerful result in symplectic geometry is Darboux’s Theorem:

Any symplectic manifold is locally equivalent to standard phase space.

This means that locally, every symplectic manifold can be described with coordinates \( (q_i, p_i) \) where the symplectic form takes its standard form.

There is no “curvature” in symplectic geometry — all local symplectic spaces look alike.

---

11. Symplectic Manifolds in Higher Dimensions

In multi-particle systems, phase space becomes very high-dimensional.

• 3D particle: 6D phase space
• Two particles in 3D: 12D phase space
• Fields: Infinite-dimensional symplectic manifolds

Despite the complexity, the symplectic structure provides the organizing principle for dynamics.

---

12. Applications in Physics

Symplectic geometry appears in:

• Classical mechanics: Structure-preserving transformations
• Quantum mechanics: Geometric quantization, phase space formulations
• Statistical mechanics: Liouville measure for ensembles
• Celestial mechanics: Integrable systems, Poincaré sections
• Field theory: Hamiltonian formulations of electrodynamics, general relativity
• Geometric optics and control theory

---

13. Conclusion

Phase space and symplectic geometry provide a powerful lens through which to view classical mechanics. They replace vector-based equations with geometric flows, emphasizing structure and conservation.

Their concepts are fundamental not only in classical systems but also in the foundations of modern physics, including quantum theory, relativity, and beyond.

Table of Contents

1. Introduction
2. What Are Poisson Brackets?
3. Mathematical Definition
4. Physical Meaning
5. Properties of Poisson Brackets
6. The Role in Hamilton’s Equations
7. Poisson Brackets and Constants of Motion
8. Symmetries and Noether’s Theorem
9. Common Poisson Brackets in Mechanics
10. Examples: Angular Momentum Algebra
11. Comparison to Commutators in Quantum Mechanics
12. Applications in Classical and Quantum Physics
13. Conclusion

---

1. Introduction

Poisson brackets are a central algebraic structure in classical mechanics. They encode how functions on phase space interact dynamically and serve as a precursor to quantum mechanical commutators.

Just as Newton gave us \( F = ma \), and Lagrange reframed it using energy functions, Hamilton’s mechanics uses Poisson brackets to describe the flow of observables in phase space. They are crucial to understanding conservation laws, symmetries, and transitions to quantum theory.

---

2. What Are Poisson Brackets?

A Poisson bracket is an operation that takes two functions \( f(q, p, t) \) and \( g(q, p, t) \) on phase space and returns another function:

\[
\{f, g\}
\]

It measures the dynamical relationship between \( f \) and \( g \) under Hamiltonian evolution.

---

3. Mathematical Definition

Let ( f ) and ( g ) be functions of canonical coordinates \( q_i \) and momenta \( p_i \). The Poisson bracket is defined as:

\[
\{f, g\} = \sum_{i} \left( \frac{\partial f}{\partial q_i} \frac{\partial g}{\partial p_i} – \frac{\partial f}{\partial p_i} \frac{\partial g}{\partial q_i} \right)
\]

---

4. Physical Meaning

The Poisson bracket tells us how two observables influence each other’s evolution.

If \( H \) is the Hamiltonian, then the time evolution of an observable \( f \) is:

\[
\frac{df}{dt} = \{f, H\} + \frac{\partial f}{\partial t}
\]

This is analogous to the Heisenberg equation in quantum mechanics, where the commutator with the Hamiltonian governs time evolution.

---

5. Properties of Poisson Brackets

Poisson brackets satisfy several key properties:

1. Bilinearity:
   \[
   \{af + bg, h\} = a\{f, h\} + b\{g, h\}
   \]
2. Antisymmetry:
   \[
   \{f, g\} = -\{g, f\}
   \]
3. Leibniz Rule:
   \[
   \{fg, h\} = f\{g, h\} + g\{f, h\}
   \]
4. Jacobi Identity:
   \[ \{f, {g, h}} + {g, {h, f}} + {h, {f, g}} = 0 ]

These properties make Poisson brackets a Lie algebra over functions on phase space.

---

6. The Role in Hamilton’s Equations

Hamilton’s equations for a system with Hamiltonian \(H(q, p)\) can be written using Poisson brackets:

\[
\dot{q}_i = \{q_i, H\}, \quad \dot{p}_i = \{p_i, H\}
\]

This means the phase space flow is generated algebraically by HHH. The Poisson bracket becomes the fundamental tool for computing the system’s evolution.

---

7. Poisson Brackets and Constants of Motion

One of the most powerful uses of Poisson brackets is in identifying constants of motion.

Let \(f(q, p, t)\)be an observable.

If:

\[
\frac{df}{dt} = \{f, H\} + \frac{\partial f}{\partial t} = 0
\]

and \( \frac{\partial f}{\partial t} = 0 \), then:

\[
\{f, H\} = 0
\]

This means \( f \) is a constant of motion.

Thus, if the Poisson bracket of a function with the Hamiltonian vanishes, that function is conserved.

This is the algebraic foundation for conservation of energy, momentum, angular momentum, and more.

---

8. Symmetries and Noether’s Theorem

In Lagrangian mechanics, Noether’s theorem connects symmetries to conservation laws.

In Hamiltonian mechanics, the connection is:

Symmetry ↔ Generator ↔ Conserved Quantity

For example:

• Translational symmetry → momentum conserved → generated by \(\{x, p\} = 1\)
• Rotational symmetry → angular momentum conserved → generated by \(\{x, L_z\}\)

Each symmetry transformation has a generator whose Poisson bracket with other quantities describes the transformation.

Each symmetry has a generator \( G \) such that:

\[
\{f, G\}
\]

describes the infinitesimal transformation of \( f \) under that symmetry.

---

9. Common Poisson Brackets in Mechanics

Some standard Poisson brackets in one dimension:

\[
\{q, q\} = 0, \quad \{p, p\} = 0, \quad \{q, p\} = 1
\]

In 3D angular momentum:

\[
\{L_x, L_y\} = L_z, \quad \{L_y, L_z\} = L_x, \quad \{L_z, L_x\} = L_y
\]

This algebra mirrors the Lie algebra of the rotation group SO(3).

---

10. Examples: Angular Momentum Algebra

Let:

\[
L_x = yp_z – zp_y, \quad L_y = zp_x – xp_z, \quad L_z = xp_y – yp_x
\]

Then:

\[
\{L_x, L_y\} = L_z, \quad \{L_y, L_z\} = L_x, \quad \{L_z, L_x\} = L_y
\]

These relations reflect the rotational symmetry of 3D space and form the basis for angular momentum theory in both classical and quantum mechanics.

---

11. Comparison to Commutators in Quantum Mechanics

In quantum theory:

\[
[\hat{f}, \hat{g}] = i\hbar \widehat{\{f, g\}}
\]

That is, the commutator of two operators corresponds to the Poisson bracket of the classical observables they represent.

Poisson brackets are thus the classical limit of quantum mechanics.

---

12. Applications

• Identifying conserved quantities in complex systems
• Deriving symmetry groups in field theories
• Transitioning to quantum mechanics via canonical quantization
• Modeling phase space evolution
• Designing integrable systems (e.g., Liouville integrability)

In short, Poisson brackets are foundational in nearly all areas of analytical mechanics and theoretical physics.

---

13. Conclusion

Poisson brackets are more than a mathematical construct — they represent the algebra of classical dynamics. By revealing constants of motion, symmetries, and generator relationships, they unify mechanics and set the stage for quantum theory.

To master them is to gain fluency in the underlying language of physics — a language that connects motion, conservation, and transformation in one coherent algebraic framework.

Table of Contents

1. Introduction
2. What Are Canonical Transformations?
3. Motivation: Why Use Canonical Transformations?
4. The Symplectic Structure
5. Poisson Brackets and Invariance
6. The Fundamental Condition for Canonicity
7. Examples of Canonical Transformations
8. Generating Functions: The Heart of Canonical Changes
9. The Four Types of Generating Functions
10. Hamilton’s Equations Under Transformation
11. Physical Meaning and Applications
12. Canonical Transformations in Quantum Mechanics
13. Conclusion

---

1. Introduction

In Hamiltonian mechanics, canonical transformations are changes of variables in phase space that preserve the form of Hamilton’s equations. These transformations lie at the heart of advanced classical mechanics and play a major role in quantum mechanics, statistical mechanics, and symplectic geometry.

By shifting from (\(q, p\)) to new variables (\(Q, P\)), we can simplify problems, reveal conserved quantities, or set up systems for quantization — without altering the underlying physics.

---

2. What Are Canonical Transformations?

A canonical transformation is a transformation of coordinates and momenta:

\[
(q_i, p_i) \rightarrow (Q_i, P_i)
\]

such that the new variables \( Q_i, P_i \) satisfy the same Hamiltonian structure as the old ones. In particular, the new Hamilton’s equations are:

\[
\dot{Q}_i = \frac{\partial H’}{\partial P_i}, \quad \dot{P}_i = -\frac{\partial H’}{\partial Q_i}
\]

for some transformed Hamiltonian \( H'(Q, P, t) \).

---

3. Motivation: Why Use Canonical Transformations?

Canonical transformations can:

• Simplify complex Hamiltonians
• Turn a non-separable system into a separable one
• Help identify constants of motion
• Connect classical and quantum mechanics
• Provide better coordinate systems for integrable problems

In short, they are like rotations or scalings in phase space that preserve the system’s dynamical essence.

---

4. The Symplectic Structure

Hamiltonian mechanics lives in a symplectic manifold, where the area (or higher-dimensional volume) in phase space is conserved.

The symplectic 2-form is:

\[
\omega = \sum_i dq_i \wedge dp_i
\]

A transformation is canonical if it preserves this structure:

\[
\omega’ = \omega
\]

This geometric idea underlies the algebraic condition that Poisson brackets remain unchanged.

---

5. Poisson Brackets and Invariance

For a transformation to be canonical, it must preserve Poisson brackets:

\[
{Q_i, Q_j} = 0, \quad {P_i, P_j} = 0, \quad {Q_i, P_j} = \delta_{ij}
\]

This ensures that the algebra of observables (functions of ( q, p )) remains consistent after transformation.

---

6. The Fundamental Condition for Canonicity

Let us denote the transformation:

\[
q_i, p_i \rightarrow Q_i(q, p), P_i(q, p)
\]

Then the transformation is canonical if and only if the Poisson bracket structure is preserved, or equivalently:

\[
\sum_i dQ_i \wedge dP_i = \sum_i dq_i \wedge dp_i
\]

---

7. Examples of Canonical Transformations

Example 1: Simple Scaling

Let:

\[
Q = \alpha q, \quad P = \frac{p}{\alpha}
\]

Then:

\[
{Q, P} = \left{ \alpha q, \frac{p}{\alpha} \right} = 1
\]

Thus, this is a canonical transformation for any nonzero \( \alpha \).

Example 2: Interchange

Let:

\[
Q = p, \quad P = -q
\]

This transformation flips position and momentum and is also canonical:

\[
{Q, P} = {p, -q} = 1
\]

---

8. Generating Functions: The Heart of Canonical Changes

A powerful way to define canonical transformations is through generating functions.

A generating function \( F \) is a function of old and new variables that implicitly defines the transformation.

There are four standard types:

• \( F_1(q, Q, t) \)
• \( F_2(q, P, t) \)
• \( F_3(p, Q, t) \)
• \( F_4(p, P, t) \)

---

9. The Four Types of Generating Functions

Let’s describe each in brief:

Type 1: \( F_1(q, Q, t) \)

\[
p_i = \frac{\partial F_1}{\partial q_i}, \quad P_i = -\frac{\partial F_1}{\partial Q_i}
\]

Type 2: \( F_2(q, P, t) \)

\[
p_i = \frac{\partial F_2}{\partial q_i}, \quad Q_i = \frac{\partial F_2}{\partial P_i}
\]

Type 3: \( F_3(p, Q, t) \)

\[
q_i = -\frac{\partial F_3}{\partial p_i}, \quad P_i = -\frac{\partial F_3}{\partial Q_i}
\]

Type 4: \( F_4(p, P, t) \)

\[
q_i = -\frac{\partial F_4}{\partial p_i}, \quad Q_i = \frac{\partial F_4}{\partial P_i}
\]

Each type connects old and new variables via derivatives of \( F \).

---

10. Hamilton’s Equations Under Transformation

Under a canonical transformation, Hamilton’s equations preserve their form, although the Hamiltonian may change.

If the generating function is explicitly time-dependent, the transformed Hamiltonian becomes:

\[
H’ = H + \frac{\partial F}{\partial t}
\]

This makes canonical transformations extremely useful for time-dependent systems or simplifying the dynamics of complex Hamiltonians.

---

11. Physical Meaning and Applications

Canonical transformations don’t alter the physical content — they relabel the system in a more convenient or insightful way.

Applications include:

• Action-angle variables in integrable systems
• Simplifying orbital dynamics in celestial mechanics
• Quantum canonical quantization (preserving commutation relations)
• Statistical mechanics (ensemble invariance)

---

12. Canonical Transformations in Quantum Mechanics

In quantum mechanics:

• Canonical transformations correspond to unitary transformations.
• Poisson brackets become commutators:

\[
{q, p} = 1 \quad \rightarrow \quad [\hat{q}, \hat{p}] = i\hbar
\]

Preserving the bracket structure is essential for valid quantization. So, classical canonical transformations must be compatible with quantum algebra.

---

13. Conclusion

Canonical transformations are not just clever coordinate changes — they preserve the entire dynamical structure of Hamiltonian mechanics. By retaining the form of the equations and Poisson brackets, they allow deeper insight into conserved quantities, symmetry, and the transition to quantum theory.

Mastering canonical transformations opens doors to more elegant physics, advanced solution techniques, and a greater understanding of symmetry and structure in both classical and quantum realms.