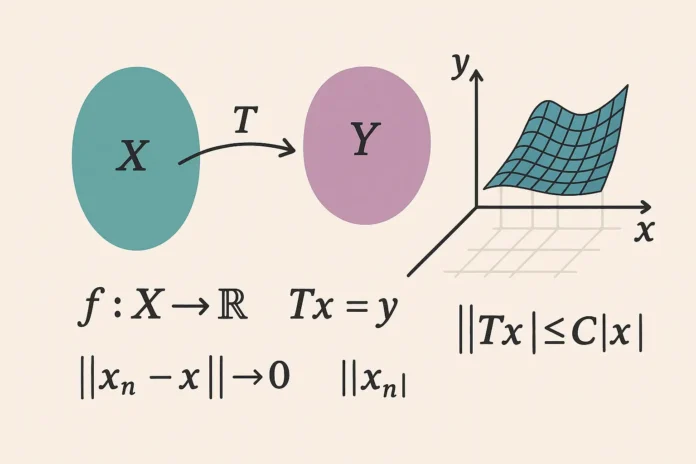Table of Contents

1. Introduction
2. What Is Topology?
3. Topological Spaces and Open Sets
4. Basis and Subbasis for a Topology
5. Closed Sets and Limit Points
6. Continuity in Topological Terms
7. Homeomorphisms and Topological Invariants
8. Compactness: Definition and Intuition
9. Sequential Compactness and Heine–Borel Theorem
10. Compactness in Metric and Topological Spaces
11. Connectedness and Path Connectedness
12. Hausdorff Spaces and Separation Axioms
13. Product and Subspace Topologies
14. Compactness in Functional Analysis and Quantum Physics
15. Conclusion

---

1. Introduction

Topology is the study of spatial properties that remain invariant under continuous deformations. Compactness is a central concept in topology and analysis, capturing the idea of “boundedness plus completeness” without relying on metrics. Both ideas are essential in theoretical physics, quantum field theory, and functional analysis.

---

2. What Is Topology?

A topology on a set \( X \) is a collection \( \mathcal{T} \) of subsets of \( X \) (called open sets) satisfying:

1. \( \emptyset, X \in \mathcal{T} \)
2. Arbitrary unions of sets in \( \mathcal{T} \) are in \( \mathcal{T} \)
3. Finite intersections of sets in \( \mathcal{T} \) are in \( \mathcal{T} \)

The pair \( (X, \mathcal{T}) \) is called a topological space.

---

3. Topological Spaces and Open Sets

Examples of topologies:

• Discrete topology: all subsets are open
• Trivial topology: only \( \emptyset \) and \( X \) are open
• Standard topology on \( \mathbb{R} \): open intervals \( (a, b) \)

Open sets generalize the idea of neighborhoods around points.

---

4. Basis and Subbasis for a Topology

A basis \( \mathcal{B} \) for a topology is a collection of open sets such that every open set is a union of basis elements.

A subbasis \( \mathcal{S} \) is a collection of subsets whose finite intersections generate a basis.

---

5. Closed Sets and Limit Points

• A closed set is the complement of an open set.
• A limit point of a set \( A \subset X \) is a point where every open neighborhood intersects \( A \setminus \{x\} \)

The closure of \( A \), denoted \( \overline{A} \), is the smallest closed set containing \( A \).

---

6. Continuity in Topological Terms

A function \( f: X \to Y \) between topological spaces is continuous if the preimage of every open set in \( Y \) is open in \( X \):

\[
f \text{ is continuous } \iff \forall U \subset Y, \ U \text{ open } \Rightarrow f^{-1}(U) \text{ is open in } X
\]

---

7. Homeomorphisms and Topological Invariants

• A homeomorphism is a bijective, continuous map with continuous inverse.
• Two spaces are topologically equivalent (homeomorphic) if there exists a homeomorphism between them.

Topological invariants (like compactness, connectedness) remain unchanged under homeomorphisms.

---

8. Compactness: Definition and Intuition

A topological space \( X \) is compact if every open cover has a finite subcover.

This generalizes the idea of bounded and closed sets in Euclidean space.

---

9. Sequential Compactness and Heine–Borel Theorem

• A space is sequentially compact if every sequence has a convergent subsequence.
• In \( \mathbb{R}^n \), compactness ⇔ closed and bounded (Heine–Borel Theorem)

---

10. Compactness in Metric and Topological Spaces

In metric spaces, compactness implies:

• Completeness
• Total boundedness
• Sequential compactness

However, in general topological spaces, these properties are not equivalent.

---

11. Connectedness and Path Connectedness

• A space is connected if it cannot be split into two disjoint open sets.
• Path connected: any two points can be joined by a continuous path

Path connected ⇒ connected, but not always vice versa.

---

12. Hausdorff Spaces and Separation Axioms

A space is Hausdorff (T2) if for any two distinct points, there exist disjoint open neighborhoods.

Important because:

• Limits are unique
• Most physical spaces modeled are Hausdorff

Other axioms: T0, T1, regular, normal spaces

---

13. Product and Subspace Topologies

• Subspace topology: inherited topology from a parent space
• Product topology: basis = product of open sets from component spaces

Used to define spaces like \( \mathbb{R}^\infty \), Hilbert cubes, and infinite function spaces.

---

14. Compactness in Functional Analysis and Quantum Physics

• Compact operators behave like finite-dimensional ones
• Weak compactness is essential in variational methods
• In quantum field theory, compactness of group manifolds (like SU(2)) affects quantization

Compactness ensures existence of solutions, boundedness of spectra, and convergence.

---

15. Conclusion

Topology and compactness offer a powerful abstract language to describe continuity, convergence, and structure in mathematics and physics. These concepts provide the underlying framework for analysis, geometry, and quantum theory, playing a key role in modern scientific understanding.

---

Table of Contents

1. Introduction
2. What Is Functional Analysis?
3. Normed and Banach Spaces
4. Inner Product and Hilbert Spaces
5. Linear Operators and Functionals
6. Bounded and Unbounded Operators
7. Dual Spaces and the Hahn–Banach Theorem
8. The Riesz Representation Theorem
9. Compact Operators and Spectral Theory
10. Self-Adjoint, Unitary, and Normal Operators
11. Hilbert–Schmidt and Trace Class Operators
12. Fourier Analysis in Hilbert Spaces
13. Applications to PDEs and Quantum Mechanics
14. Weak and Strong Convergence
15. Conclusion

---

1. Introduction

Functional analysis generalizes linear algebra and calculus to infinite-dimensional vector spaces. It is the mathematical foundation of quantum mechanics, partial differential equations (PDEs), and signal processing. It brings together vector spaces, topology, and linear operators in a unified framework.

---

2. What Is Functional Analysis?

Functional analysis studies vector spaces of functions and linear operators acting on them. Central themes include:

• Infinite-dimensional spaces
• Continuity and boundedness
• Spectral theory of operators
• Duality and convergence

---

3. Normed and Banach Spaces

A normed vector space \( (X, |\cdot|) \) is a vector space with a norm satisfying:

1. \( |x| \ge 0 \), and \( |x| = 0 \iff x = 0 \)
2. \( |\alpha x| = |\alpha||x| \)
3. \( |x + y| \le |x| + |y| \) (triangle inequality)

A Banach space is a complete normed space — all Cauchy sequences converge.

---

4. Inner Product and Hilbert Spaces

An inner product \( \langle x, y \rangle \) satisfies:

1. \( \langle x, x \rangle \ge 0 \)
2. \( \langle x, x \rangle = 0 \iff x = 0 \)
3. \( \langle x, y \rangle = \overline{\langle y, x \rangle} \)
4. Linearity in the first argument

The induced norm is \( |x| = \sqrt{\langle x, x \rangle} \)

A Hilbert space is a complete inner product space.

---

5. Linear Operators and Functionals

A linear operator \( T: X \to Y \) satisfies:

\[
T(\alpha x + \beta y) = \alpha T(x) + \beta T(y)
\]

A functional is a map \( f: X \to \mathbb{F} \) (usually \( \mathbb{R} \) or \( \mathbb{C} \)).

---

6. Bounded and Unbounded Operators

• Bounded: there exists \( C > 0 \) such that \( |Tx| \le C|x| \)
• Unbounded: no such constant exists; common in differential operators

Bounded operators are continuous; unbounded ones must be treated carefully.

---

7. Dual Spaces and the Hahn–Banach Theorem

The dual space \( X^* \) consists of all bounded linear functionals on \( X \).

Hahn–Banach Theorem: extends a bounded functional from a subspace to the whole space without increasing the norm.

---

8. The Riesz Representation Theorem

For a Hilbert space \( H \), every bounded linear functional \( f \in H^* \) is uniquely represented as:

\[
f(x) = \langle x, y \rangle \quad \text{for some } y \in H
\]

This establishes an isomorphism between \( H \) and \( H^* \).

---

9. Compact Operators and Spectral Theory

A compact operator maps bounded sets to relatively compact sets. In Hilbert spaces, these operators resemble matrices with countable spectra.

Spectral theory studies eigenvalues and eigenvectors of operators:

• Spectrum \( \sigma(T) \): generalization of eigenvalues
• Resolvent set: \( \lambda \in \mathbb{C} \) where \( (T – \lambda I)^{-1} \) exists

---

10. Self-Adjoint, Unitary, and Normal Operators

• Self-adjoint: \( T = T^* \)
• Unitary: \( T^T = TT^ = I \)
• Normal: \( TT^* = T^*T \)

Self-adjoint operators correspond to observables in quantum mechanics.

---

11. Hilbert–Schmidt and Trace Class Operators

• Hilbert–Schmidt: \( \sum |Te_n|^2 < \infty \)
• Trace class: \( \sum \langle Te_n, e_n \rangle < \infty \)

These operators are compact and play a role in quantum statistical mechanics.

---

12. Fourier Analysis in Hilbert Spaces

In \( L^2(\mathbb{R}) \), functions can be expanded as orthonormal sums:

\[
f(x) = \sum_{n} \langle f, e_n \rangle e_n(x)
\]

Fourier basis provides a canonical orthonormal set in function spaces.

---

13. Applications to PDEs and Quantum Mechanics

• Weak solutions to PDEs
• Variational methods and Sobolev spaces
• Quantum observables as self-adjoint operators
• Schrödinger equation in Hilbert space form
• Spectral decomposition and time evolution

---

14. Weak and Strong Convergence

• Strong convergence: \( |x_n – x| \to 0 \)
• Weak convergence: \( f(x_n) \to f(x) \) for all \( f \in X^* \)

Weak convergence is weaker but still useful in compactness and variational problems.

---

15. Conclusion

Functional analysis provides a rigorous mathematical framework for studying infinite-dimensional systems and operators. It is indispensable in quantum mechanics, PDE theory, and modern applied mathematics. Mastery of its basic concepts is a gateway to understanding advanced theoretical frameworks in both physics and analysis.

---

Table of Contents

1. Introduction
2. What Is a Tensor?
3. Scalars, Vectors, and Higher-Rank Tensors
4. Tensor Notation and Index Conventions
5. Contravariant and Covariant Tensors
6. The Metric Tensor and Index Raising/Lowering
7. Tensor Transformation Laws
8. Symmetry and Antisymmetry in Tensors
9. Tensor Operations: Addition, Contraction, Outer Products
10. Covariant Derivatives and the Connection Coefficients
11. The Riemann Curvature Tensor
12. Ricci Tensor and Scalar Curvature
13. Einstein Tensor and Einstein Field Equations
14. Tensors in Special and General Relativity
15. Applications in Continuum Mechanics and Electromagnetism
16. Conclusion

---

1. Introduction

Tensors are the mathematical backbone of modern physics, providing a coordinate-independent language to express physical laws. Tensor analysis enables the formulation of theories like general relativity, electromagnetism, and fluid dynamics in a geometric and covariant framework.

---

2. What Is a Tensor?

A tensor is a geometric object that generalizes scalars and vectors, and transforms in a specific way under coordinate transformations.

A tensor of rank \( (r, s) \) has \( r \) contravariant (upper) and \( s \) covariant (lower) indices:

\[
T^{\mu_1 \dots \mu_r}_{\nu_1 \dots \nu_s}
\]

---

3. Scalars, Vectors, and Higher-Rank Tensors

• Scalar: rank-0 tensor, invariant under transformations
• Vector: rank-1 tensor with one upper index \( V^\mu \)
• Covector (dual vector): rank-1 tensor with one lower index \( V_\mu \)
• Rank-2 tensor: \( T^{\mu\nu}, T^\mu{}\nu, T{\mu\nu} \), etc.

---

4. Tensor Notation and Index Conventions

Einstein summation convention: repeated upper and lower indices are summed:

\[
A^\mu B_\mu = \sum_\mu A^\mu B_\mu
\]

Latin indices typically denote spatial dimensions, Greek for spacetime.

---

5. Contravariant and Covariant Tensors

• Contravariant: transforms with inverse Jacobian:

\[
V’^\mu = \frac{\partial x’^\mu}{\partial x^\nu} V^\nu
\]

• Covariant: transforms with Jacobian:

Mixed tensors combine both types.

---

6. The Metric Tensor and Index Raising/Lowering

The metric tensor \( g_{\mu\nu} \) maps vectors to covectors and defines inner products:

\[
V_\mu = g_{\mu\nu} V^\nu, \quad V^\mu = g^{\mu\nu} V_\nu
\]

It also defines distances and angles:

\[
ds^2 = g_{\mu\nu} dx^\mu dx^\nu
\]

---

7. Tensor Transformation Laws

A tensor of type \( (r, s) \) transforms as:

---

8. Symmetry and Antisymmetry in Tensors

• Symmetric: \( T_{\mu\nu} = T_{\nu\mu} \)
• Antisymmetric: \( T_{\mu\nu} = -T_{\nu\mu} \)

Antisymmetric rank-2 tensors are used to define quantities like the electromagnetic field tensor.

---

9. Tensor Operations: Addition, Contraction, Outer Products

• Addition: valid for tensors of the same type
• Contraction: sum over one upper and one lower index, reduces rank
• Outer product: combines tensors into higher-rank tensors

---

10. Covariant Derivatives and the Connection Coefficients

Ordinary derivatives do not preserve tensor character under transformations.

The covariant derivative \( \nabla_\mu \) includes connection coefficients (Christoffel symbols \( \Gamma^\lambda_{\mu\nu} \)):

\[
\nabla_\mu V^\nu = \partial_\mu V^\nu + \Gamma^\nu_{\mu\lambda} V^\lambda
\]

---

11. The Riemann Curvature Tensor

Measures the noncommutativity of covariant derivatives:

Encodes the intrinsic curvature of spacetime.

---

12. Ricci Tensor and Scalar Curvature

• Ricci tensor: contraction of Riemann tensor:

\[
R_{\mu\nu} = R^\lambda{}_{\mu\lambda\nu}
\]

• Ricci scalar: contraction of Ricci tensor with the metric:

\[
R = g^{\mu\nu} R_{\mu\nu}
\]

---

13. Einstein Tensor and Einstein Field Equations

The Einstein tensor:

\[
G_{\mu\nu} = R_{\mu\nu} – \frac{1}{2} g_{\mu\nu} R
\]

Einstein’s field equations:

\[
G_{\mu\nu} = \frac{8\pi G}{c^4} T_{\mu\nu}
\]

Relates curvature of spacetime to energy and momentum.

---

14. Tensors in Special and General Relativity

• Special relativity: Minkowski metric \( \eta_{\mu\nu} \), 4-vectors
• General relativity: dynamic spacetime metric \( g_{\mu\nu}(x) \), curvature tensors

Tensors ensure the general covariance of physical laws.

---

15. Applications in Continuum Mechanics and Electromagnetism

• Stress-energy tensor: describes energy, momentum, and stress in a field
• Electromagnetic field tensor:

\[
F_{\mu\nu} = \partial_\mu A_\nu – \partial_\nu A_\mu
\]

Tensors also describe strain, stress, and deformation in solid mechanics.

---

16. Conclusion

Tensor analysis provides a powerful and consistent language to describe physical laws in any coordinate system. From general relativity to electromagnetism, it allows elegant and coordinate-independent formulations of complex systems.

Mastery of tensors is crucial for modern theoretical physics and applied mathematical modeling.

---